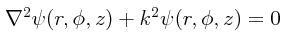La solución matemática de la ecuación de onda depende directamente de la naturaleza de la función del potencial V(x). Sin lugar a dudas el caso más sencillo será aquél en el cual la función de onda es igual a una constante, y este será nuestro punto de entrada al análisis que será llevado a cabo de esta ecuación diferencial.
PROBLEMA: Resuélvase la ecuación:
considerando tanto a V como a E como constantes.
Podemos tomar la ecuación diferencial escribiéndola de la siguiente manera:
Puesto que la masa es una constante positiva (ignorando por lo pronto posibles efectos relativistas) al igual que la constante reducida de Planck, la solución de esta ecuación dependerá del hecho de que el factor V-E que aparece en el lado derecho de la ecuación sea positivo o negativo. Haciendo:
tenemos entonces la siguiente ecuación diferencial de segundo orden:
Empleando notación operacional haciendo D² = d²/dx², lo anterior se puede escribir simplemente como:
En la teoría elemental de las ecuaciones diferenciales se aprende que la ecuación auxiliar para la ecuación diferencial homogénea es:
siendo la solución general de la ecuación diferencial la siguiente:
y siendo A y B dos constantes.
Tenemos dos posibilidades: la primera consiste en que V sea mayor que E, en cuyo caso el radicando en ambos términos será positivo y la exponenciación se llevará a cabo hacia un exponente real, y la segunda consiste en que V sea menor que E, en cuyo caso el radicando en ambos términos será negativo y la exponenciación se llevará a cabo hacia un exponente imaginario.
Considérese primero el caso en el que V es mayor que E.
No cuesta mucho trabajo el comprobar que el primer término de la solución general es en efecto una solución matemática aceptable a la ecuación diferencial original de segundo orden:
Tampoco involucra mayores dificultades el comprobar que el segundo término de la solución general también es una solución matemática aceptable a la ecuación diferencial original de segundo orden:
Ambas términos son soluciones matemáticamente aceptables. Sin embargo, no tardamos mucho tiempo en darnos cuenta de que el primer término presenta una dificultad insalvable. Aún antes de intentar darle una interpretación física a ψ(x), podemos ver que para el caso en el cual V es mayor que E, con lo cual la cantidad dentro del radical es positiva, el primer término va creciendo exponencialmente para valores cada vez mayores de la variable independiente. Si suponemos que la “cantidad de materia” está relacionada de alguna manera con la magnitud de ψ(x), en forma tal que en donde ψ(x) tiene un valor de cero no habrá presencia de materia alguna y en donde ψ(x) tiene un valor grande habrá una presencia mayor de materia, entonces el incremento exponencial de ψ(x) convierte al primer término en algo que eventualmente tenemos que desechar por carecer de significado físico. En pocas palabras, una solución matemática aceptable a una ecuación diferencial no necesariamente representa una solución aceptable cuando se le pretende dar significado físico en el mundo real. El segundo término no presenta este problema porque en virtud del signo negativo en el exponencial dicho término decrece exponencialmente volviéndose prácticamente igual a cero inclusive para valores moderadamente altos de la variable independiente. Esto nos revela que la ecuación de Schrödinger puede tener como solución aceptable una función de onda que decrece exponencialmente.
Considérese ahora el caso en el que V es menor que E.
Siempre que tenemos el número e elevado a un argumento imaginario podemos recurrir al teorema de DeMoivre que nos garantiza que podemos substituír la expresión exponencial por una expresión compleja que combina un término real y un término imaginario:
Trabajando nuevamente sobre el primer término de la solución general a la ecuación de onda y usando el término cosenoidal de acuerdo a lo que nos indica el teorema de DeMoivre, resulta fácil comprobar que el primer término de la solución general es en efecto una solución matemática aceptable a la ecuación diferencial original de segundo orden cuando V es menor que E:
El signo negativo que ha aparecido en este último paso no es de consecuencia alguna, porque tomando en cuenta que hemos partido de la hipótesis de que V es menor que E, el signo negativo se encarga de restaurar el lado derecho de la ecuación diferencial a su condición de signo positivo.
Obviamente, para el caso en el que V es menor que E, tenemos una solución oscilatoria, la cual es aceptable desde el punto de vista matemático. Aunque la solución matemática de la ecuación de onda para el caso en el que V es menor que E no es una cosa que crezca exponencialmente más allá de todo límite, esta solución nos presenta una situación algo incómoda, porque permite que ψ(x) se pueda extender hacia el infinito en ambas direcciones sobre el eje coordenado-x sin volverse cero jamás, lo cual contradice nuestra noción básica de que una partícula puede ser localizada dentro de cierta región del espacio con cierto grado de probabilidad aún con todo y el principio de incertidumbre. Sin embargo, si acotamos la función ψ(x) dentro de un intervalo finito de modo tal que no se pueda extender indefinidamente fuera de este intervalo al hacerla fuera de dicho intervalo, entonces tenemos una solución matemática que también puede poseer un significado físico, en este caso, un comportamiento oscilatorio. Esto nos revela que la ecuación de Schrödinger puede tener como solución aceptable una función de onda oscilante.
Puesto que un potencial V(x) que no sea igual a una constante de cualquier modo tiene que tener en cada punto a lo largo de un eje coordenado-x horizontal un valor que necesariamente será mayor o menor que E, en base a lo que hemos obtenido arriba podemos intuír que todas las soluciones a la ecuación de onda estarán prefijadas a ser ya sea funciones exponencialmente decrecientes u oscilatorias. Más aún, dada cualquier función de potencial V(x), por complicada que esta sea podemos sub-dividir el eje coordenado horizontal en regiones de modo tal que dentro de ciertas regiones V siempre será menor que E mientras que en las otras regiones V siempre será mayor que E, teniendo un comportamiento oscilatorio en unas y un comportamiento exponencialmente decreciente en otras. Naturalmente, al pasar de una región a otra, la función ψ(x) tiene que tener el mismo valor en el punto de contacto entre ambas regiones como requisito básico de continuidad, ya que de lo contrario estaríamos hablando de partículas diferentes o sistemas físicos diferentes y no de un mismo sistema físico o de una misma partícula. Pero no basta con que en el punto de contacto entre dos regiones distintas proporciones para ambas regiones el mismo valor de ψ(x). Se requiere también que la “velocidad” de cambio de ψ(x) al pasar de una región a otra, esto es, dψ(x)/dx, sea el mismo. Pero estos ya no son requisitos meramente matemáticos para darle una solución aceptable a una función de onda a través de varias regiones, se trata de requerimientos de índole física.
De este modo, podemos especificar cuatro condiciones que toda función ψ(x) que sea una solución matemática a la ecuación de Schrödinger debe cumplir para poder ser una solución físicamente admisible:
1) ψ(x) debe satisfacer la ecuación de onda de Schrödinger.
2) ψ(x) debe ser una función continua.
3) dψ(x)/dx debe ser continua.
4) ψ(x).→.0 conforme x.→.±.∞
Consideraremos ahora el caso en el cual el potencial V(x) no es necesariamente igual a una constante. Una situación que se presta a un análisis matemático simplificado es la de un pozo de potencial especificado de la siguiente manera:
___V(x) = 0__para |x|<a
___V(x) es cualquier función tal que V(x)>E para |x|>a
Además de las dos condiciones anteriores, impondremos una condición de simetría:
___V(-x) = V(x)
Gráficamente, la condición de simetría que hace que el valor de V(x) sea el mismo en -x que en +x, de forma tal que la función se verá como si estuviese reflejada ante un espejo con respecto al eje vertical en x = 0. Se dice que este tipo de funciones tienen paridad par o una paridad de +1, mientras que funciones para las cuales V(-x) = -V(x) tienen paridad impar o una paridad de -1. La condición de simetría nos permite concentrarnos en las soluciones de la ecuación de Schrödinger para valores positivos de la variable independiente (la coordenada horizontal-x) ya que las soluciones para valores negativos de la variable independiente serán las mismas. Para una partícula cuya energía total es E, podemos bosquejar en términos generales un pozo de potencial de la manera siguiente:
Clásicamente, una partícula estará confinada a moverse dentro de una región para la cual su energía E es mayor que la energía potencial, o sea -a<x<+a. Puesto que hemos especificado que el potencial tenga un valor V(x) = 0 en esta región, la ecuación de Schrödinger queda escrita de la siguiente manera:
lo cual podemos escribir como:
Esta ecuación diferencial de segundo orden tiene dos soluciones posibles, siendo la primera solución una función de onda par:
y siendo la segunda solución una función de onda impar:
en donde λ = 2π/k es la longitud de onda.
Para el caso en el cual |x|>a la ecuación de Schrödinger viene siendo:
siendo:
una cantidad siempre positiva.
No podemos resolver la última ecuación diferencial a menos de que la función V(x) sea especificada. Sin embargo, lo importante de dicha ecuación es que α² siempre es positiva, y por lo tanto d²ψ/dx² tendrá el mismo signo que ψ(x). A estas alturas, siendo la ecuación de onda una ecuación diferencial de segundo orden, resulta conveniente repasar el significado matemático del signo que esté asociado con la derivada de segundo orden d²ψ/dx², lo cual tiene que ver directamente con la concavidad de la función ψ(x). Si bien la derivada de primer orden dψ/dx de la función ψ(x) nos dá la pendiente de la tangente en cada punto de la curva, el signo de la derivada de segundo orden d²ψ/dx² nos dice si la curva es cóncava hacia arriba cuando el signo es positivo (lo cual indica una pendiente o tangente siempre creciente, girando en sentido contrario al giro de las manecillas del reloj):
o si la curva es cóncava hacia abajo cuando el signo es negativo (lo cual indica una pendiente o tangente girando en el sentido de las manecillas del reloj):
De este modo, en una función hipotética como la siguiente:
podemos ver que la función es cóncava hacia arriba en los intervalos B, C y E, y es cóncava hacia abajo en los intervalos A y D. En este tipo de situaciones, hay que estar atentos siempre ante la posibilidad de que la función matemática sea tal que haya un cambio en el sentido de la concavidad, el cual ocurre en un punto de inflexión en el cual la segunda derivada de la función con respecto a la variable independiente d²ψ/dx² toma un valor igual a cero:
Resumiendo lo que se ha dicho arriba acerca de la concavidad de una función, tenemos tres situaciones:
Para un valor de d²ψ/dx² positivo, la curva será concava hacia arriba.
En un valor de d²ψ/dx² = 0, la curva cambiará de concavidad.
Para un valor de d²ψ/dx² negativo, la curva será concava hacia abajo.
PROBLEMA: Dada la siguiente función:
determínense las regiones en las cuales la función es cóncava hacia arriba así como las regiones en las cuales la función es cóncava hacia abajo, y asimismo determínense los puntos de inflexión en los cuales haya un cambio en la concavidad de la función.
Tomando la primera y la segunda derivadas de la función, obtenemos lo siguiente:
Para valores negativos de la variable independiente, más negativos que x = -4, la derivada de segundo orden d²ψ/dx² de la función ψ(x) tendrá un valor siempre positivo, razón por la cual la función será cóncava hacia arriba en la región -∞<x<-4. Para valores entre x = -4 y x = 2, d²ψ/dx² tendrá un valor siempre negativo, razón por la cual la función será cóncava hacia abajo en la región -4<x<2. Y para valores mayores que x = 2, d²ψ/dx² nuevamente tendrá un valor siempre positivo, razón por la cual la función será cóncava hacia arriba en la región 2<x<+∞. Los puntos de inflexión en los cuales la función ψ(x) cambia de concavidad obviamente son x = -4 y x = 2.
Volviendo a la ecuación de onda para el caso de una región pozo de potencial, considérese un valor arbitrario cualquiera de la energía E en la ecuación de onda. Puesto que dentro de la región |x|<a el potencial V(x) tiene un valor igual a cero, entonces la solución típica en dicha región tendrá un carácter oscilatorio. Pero fuera de dicha región podemos suponer que la continuación de la función ψ(x) “de dentro hacia afuera” tomará un comportamiento exponencial. Generalmente hablando, estos comportamientos fuera de la región |x|<a no tienden a cero para grandes valores de la abcisa (x); y la función de onda se aproxima al infinito positivo o al infinito negativo excepto para ciertos valores de E. Considérese la solución par ψ(x) = Acos(2πx/λ) para |x|<a en el caso λ/4 = 2a, o lo que es lo mismo, λ = 8a, la cual corresponde a una energía:
o bien E1 = h²/128ma². En esta situación, ψ(x) = Acos(πx/4a), y ψ(x) va disminuyendo encaminándose desde el punto x.=.0 pasando por el punto x.=.+a hasta un valor de cero con una pendiente negativa:
ψ(0) = Acos(0) = A·(1) = A
ψ(a) = Acos(πa/4a) = Acos(π/4) = A/√2
ψ(2a) = Acos(2πa/4a) = Acos(π/2) = = A·(0) = 0
El comportamiento de la función ψ(x) para la región |x|<a extendido hasta x.=.+2a es el que se muestra en el siguiente diagrama continuado con la línea punteada:
Sin embargo, fuera de la región |x|<a la solución con λ = 8a deja de ser oscilatoria porque el potencial V(x) deja de ser igual a cero, y lo que parece ser una solución aceptable porque satisface la ecuación de Schrödinger dentro del pozo de potencial no lo es, ya que aunque se encamina hacia cero en el punto x.=.+a la razón en el incremento de la pendiente d²ψ/dx² se vuelve tan grande al salir de la región |x|< que la pendiente dψ/dx eventualmente se vuelve positiva antes de que la función ψ(x) se vuelva igual a cero, con un cambio en la concavidad de la curva pasando a ser cóncava hacia arriba (como lo muestra la línea curva sólida arriba de la línea punteada) acercándose a un infinito positivo para grandes valores de la variable x. Lo que tenemos, en efecto, es un cambio en la concavidad de la solución ψ(x) = Acos(2πx/λ) con λ = 8a, siendo cóncava hacia abajo en x<a y siendo cóncava hacia arriba en x>a. El punto de inflexión está situado justo en x.=.+a .
¿Y qué pasa si vamos reduciendo gradualmente el valor de la longitud de onda λ del valor inicial λ = 8a con el que habíamos empezado? Ocurre algo muy curioso. Conforme nos vamos aproximando a un valor crítico λ1 vemos que, al igual que arriba, ψ(x).→.+.∞ para x.→.+.∞. Sin embargo, ligeramente por debajo de ese valor crítico, nos encontramos con que ψ(x).→.-.∞ para x.→.+.∞. Justo en ese valor crítico, tanto ψ(x) como dψ/dx se aproximan a cero de manera conjunta. Esto nos lo muestra con mayor claridad el siguiente diagrama:
De este modo, encontramos que hay una solución exacta con un significado físico real para la ecuación de onda, la cual corresponde a un valor crítico λ1. Pero esta no es la única solución exacta con significado físico real para la ecuación de onda que estamos considerando. Si continuamos disminuyendo el valor de λ aún más, se sigue teniendo ψ(x).→.-.∞ para x.→.+.∞ hasta que llegamos a otro valor crítico λ2 que también corresponde a otra solución aceptable. En este caso, la función de onda cruza el eje horizontal una vez y tras esto se va acercando a cero conforme x.→.+.∞. Nuevamente, justo en ese valor crítico, tanto ψ(x) como dψ/dx se aproximan a cero de manera conjunta, correspondiendo a otra energía:
Esto nos lo muestra con mayor claridad el siguiente diagrama:
Obsérvese que tanto en la curva verde como en la curva magenta hay cambios en la concavidad de ambas curvas justo en el punto x.=.+a, y en ambos casos los puntos de inflexión están situados en x.=.+a. Sin embargo, en la curva café que representa una solución físicamente admisible no hay cambio alguno en la concavidad de la solución en x.=.+a. La figura mostrada arriba es válida únicamente para los valores positivos de la coordenada-x. Sin embargo, siendo simétrica la curva con respecto a la vertical en el punto de origen de las coordenadas, podemos sin dificultad alguna visualizar el “panorama completo” tanto para valores negativos como para valores positivos de la coordenada-x con la siguiente figura ampliada:
Las dos soluciones admisibles λ1 y λ2 que han sido encontradas a la ecuación de onda no son las únicas posibles. Hay otra solución exacta con significado físico real para la ecuación de onda que corresponde a otro valor crítico λ3.Y hay otra solución exacta también con significado físico real para la ecuación de onda que corresponde a un valor crítico λ4. De hecho, hay un número infinito -pero discreto- de soluciones posibles. Cada una de estas soluciones críticas representa una solución eigen a la ecuación de onda. A estas alturas, la terminología tal vez empiece a parecer familiar para quienes hayan estudiado las soluciones a un sistema físico desde el punto de vista de la Mecánica Matricial. Pero hay una diferencia importante: las soluciones eigen que estamos obteniendo aquí son eigen-soluciones a una ecuación diferencial, no son las entradas que aparecen a lo largo de la diagonal principal de una matriz como los valores característicos de una matriz. De este modo, mientras que en la Mecánica Matricial resolvemos los problemas recurriendo a matrices, en la Mecánica Ondulatoria resolvemos los problemas recurriendo a ecuaciones diferenciales. Sin embargo, una cosa debe ser absolutamente cierta: el conjunto de soluciones que se obtienen para un sistema físico en la Mecánica Matricial debe ser igual, idéntico (no sólo parecido o similar) al conjunto de soluciones que se obtienen para el mismo sistema en la Mecánica Ondulatoria, porque si fuesen diferentes uno de ellos tendría que estar en grave error. Hasta la fecha, la concordancia entre ambas ramas de la Mecánica Cuántica se ha sostenido en pie. Y de hecho, se puede demostrar que ambas metodologías son equivalentes, aunque esto tiene que ser pospuesto hasta que el lector haya adquirido una mayor familiaridad con ambas vertientes.
Una pregunta crucial que amerita ser contestada es la siguiente: Si se obtienen dos soluciones distintas para un sistema físico mediante la ecuación de Schrödinger, correspondiendo a las dos funciones de onda distintas dos valores eigen de energías diferentes, ¿son realmente independientes dichas soluciones la una de la otra? Este es un asunto importante porque, de no serlo, podríamos terminar con una serie de dependencias en cascada que no nos llevarían a ningún lado. Pedir que las soluciones realmente sean soluciones distintas es tanto como pedir que sean ortogonales en el sentido matemático de la palabra (en el sentido geométrico, la idea es de una ortogonalidad como la medición del ancho y la altura de un cuadro, ambas dimensiones se llevan a cabo en ejes distintos independientes el uno del otro). La respuesta a la pregunta es en el sentido afirmativo, como se demostrará a continuación.
PROBLEMA: Demostrar que para dos estados ligados distintos (correspondiendo por ejemplo a una partícula atrapada en una caja) las funciones propias que pertenecen a valores propios distintos son ortogonales.
Sea ψ1 una función de onda propia que corresponda al eigenvalor de energía E1, y sea ψ2 una función de onda propia que corresponda al eigenvalor de energía E2. Si suponemos un sistema físico tridimensional descrito mediante coordenadas rectangulares Cartesianas, entonces utilizando el operador diferencial nabla:
las ecuaciones de onda de Schrödinger independientes en el tiempo para cada una de las dos funciones de onda son, respectivamente:
Si tomamos el conjugado complejo de la segunda expresión, tendremos entonces el siguiente par de ecuaciones, teniendo en mente en todo momento que E1 y E1 son reales (como ayuda visual, a la función de onda ψ1 que permanece intacta se le mostrará de color azul, mientras que a la función de onda ψ2 a la cual se le toma el conjugado complejo se le mostrará de color rojo además de agregarle el exponente asterisco que indica lo mismo):
A continuación, multiplicaremos por el lado izquierdo de la primera ecuación por ψ2*, mientras que multiplicaremos también por el lado izquierdo de la segunda ecuación por ψ1, obteniendo de este modo el siguiente sistema de ecuaciones:
Restando la segunda ecuación de la primera, el término V desaparece y tendremos lo siguiente:
A continuación, integraremos ambos lados de esta expresión sobre una región encerrada en un volumen finito:
El término entre paréntesis en la expresión del lado izquierdo de la igualdad es susceptible de una simplificación observando primero que, usando la regla de Leibniz cuando el operador diferencial nabla actúa sobre el producto de dos funciones:
Esto nos permite obtener, por separado, lo siguiente:
Restando lo segundo de lo primero tenemos entonces:
El lado izquierdo se puede agrupar aplicando la propiedad distributiva del operador diferencial nabla:
Pero el lado derecho es precisamente lo que tenemos en la ecuación que obtuvimos arriba. Podemos llevar a cabo una simplificación adicional utilizando una relación que nos viene del Análisis Vectorial, la ley de Gauss mejor conocida como el teorema de la divergencia, el cual nos permite convertir una integral de volumen en una integral de superficie cuando el integrando de la integral de volumen es la divergencia de un vector F (o, más propiamente dicho, un campo vectorial F en el cual se asigna un vector F a cada punto del espacio tridimensional bajo consideración que puede ser distinto en magnitud y sentido de los demás vectores F en otros puntos del espacio tridimensional) obtenida mediante el producto vectorial punto (producto escalar) del operador nabla y el vector F:
De este modo, llegamos a la siguiente expresión:
Obsérvese que dentro de la integral de superficie (la expresión en el lado izquierdo de la igualdad) tenemos el producto escalar entre dos vectores, siendo uno de ellos el vector:
que usando notación vectorial de tres componentes dentro de paréntesis viene siendo (escrito como la diferencia entre dos vectores):
o bien (escrito como la diferencia entre dos vectores):
y el elemento infinitesimal de superficie:
de forma tal que la integral de superficie nos viene produciendo a fin de cuentas una simple cantidad escalar (un número).
Ahora dejaremos que en la expresión que involucra en el lado izquierdo a una integral de superficie y en el lado derecho a una integral volumétrica que la superficie S en la expresión (la cual podemos imaginar como la superficie de un cubo o de una esfera) vaya creciendo yéndose hasta el infinito, de modo tal que el volumen V encerrado por dicha superficie se convierta en todo el espacio del Universo entero. Puesto que tanto la función de onda ψ1 como la función de onda ψ2 corresponden a funciones de onda de estados ligados, ambas funciones de onda deben reducirse a un valor igual a cero en el infinito, y se puede demostrar que ambas se van a cero con la suficiente rapidez como para que la integral de superficie llevada a cabo sobre la superficie S también tienda a cero cuando el volumen V que encierra se vuelve infinitamente grande. Por lo tanto se tiene lo siguiente:
Por hipótesis, E1 y E1 son reales y son diferentes, lo cual a su vez implica que:
Entonces las dos funciones de onda distintas deben ser ortogonales, a menos de que una de ellas (o ambas) sea cero.
En caso de haberse supuesto que las cantidades E1 y E2 no son cantidades reales sino complejas, habríamos tenido (E1-E2*) en el lado derecho de la penúltima ecuación. En tal caso, si ahora tomamos por ψ2 la misma función que es ψ1, con lo cual E1 y E2 serían necesariamente iguales, entonces el lado derecho de la ecuación siempre se anularía conforme la superficie S va aumentando hasta el infinito, y la integral volumétrica ya no sería igual a cero. Con esto, hemos probado también que (E1-E1*) debe ser necesariamente igual a cero, o lo que es lo mismo, E1 no puede ser un número complejo sino un número real.
Aunque por razones pedagógicas muchos ejemplos y ejercicios propios de la Mecánica Ondulatoria se llevan a cabo a lo largo de un solo eje espacial coordenado (generalmente el eje-x), en el espacio tridimensional en el que vivimos sabemos de antemano que una onda de materia requerirá para su descripción de tres coordenadas espaciales, lo cual ciertamente nos viene a complicar las cosas, sobre todo si estaremos especificando funciones de onda no en coordenadas Cartesianas rectangulares sino en algún otro tipo de coordenadas curvilíneas. Afortunadamente, para manejar situaciones de este tipo se cuenta con una técnica extraordinariamente útil conocida como el método de separación de variables, el cual consiste en tomar una expresión que está en función de tres coordenadas ortogonales (independientes) substituyendo dicha función por el producto de tres funciones que dependen cada una de ellas de una sola variable. En base a esto, si tenemos una función como Ψ(p,q,r), entonces dicha función es reemplazada por el producto de tres funciones P, Q y R:
Ψ(p,q,r) = P(p)Q(q)R(r)
Esta técnica puede ser aplicada de inmediato y en forma directa en la solución de problemas en los cuales tenemos ecuaciones diferenciales parciales tales como la ecuación de Helmholtz:
Esta ecuación surge repetidamente en la resolución de problemas de la Mecánica Ondulatoria.
PROBLEMA: Utilícese el método de separación de variables para separar la ecuación diferencial parcial de Helmholtz en tres ecuaciones diferenciales ordinarias mediante el empleo de coordenadas Cartesianas rectangulares.
Substituyendo el operador Laplaciano (nabla ó del) en la ecuación diferencial parcial de Helmholtz tal y como debe utilizarse cuando se están usando coordenadas Cartesianas rectangulares, tenemos entonces la siguiente ecuación:
En las coordenadas Cartesianas rectangulares podemos escribir:
con lo cual obtenemos lo siguiente al llevar a cabo las diferenciaciones parciales mostradas:
Del mismo modo:
Por lo tanto:
Dividiendo esto último entre ψ = XYZ y reacomodando los términos, tenemos entonces:
Puesto que las tres coordenadas Cartesianas rectangulares son independientes la una de las otras, ambos lados (izquierdo y derecho) de esta última relación tienen que ser necesariamente iguales a una constante, la cual podemos escoger como l², con lo cual logramos obtener nuestra primera separación de variables logrando así nuestra primera ecuación diferencial ordinaria:
Trabajando sobre el lado derecho de la penúltima ecuación podemos ir en pos de la segunda ecuación diferencial ordinaria:
Empleando el mismo razonamiento que usamos arriba, puesto que la coordenada-y y la coordenada-z son coordenadas independientes obtenemos la segunda ecuación diferencial ordinaria:
Finalmente:
PROBLEMA: Utilícese el método de separación de variables para separar la ecuación diferencial parcial de Helmholtz en tres ecuaciones diferenciales ordinarias mediante el empleo de coordenadas cilíndricas.
En coordenadas cilíndricas (r,φ,z), la ecuación de Helmholtz toma el siguiente aspecto:
Recurriendo al operador Laplaciano tal y como se utiliza cuando hay coordenadas cilíndricas de por medio, tenemos entonces la siguiente ecuación diferencial parcial de segundo orden:
Nuevamente, y con el propósito de llevar a cabo una separación de variables, escribimos lo siguiente:
Llevando a cabo las primeras diferenciaciones parciales, tenemos a continuación:
Del mismo modo:
Por lo tanto:
Como puede verse, todas las derivadas parciales se han convertido en derivadas ordinarias. Dividiendo entre ψ = RΦZ y procediendo como lo hicimos arriba en el caso de las coordenadas rectangulares Cartesianas:
Como puede verse, puesto que las tres coordenadas cilíndricas son independientes la una de las otras, ambos lados (izquierdo y derecho) de esta última relación tienen que ser necesariamente iguales a una constante, la cual podemos escoger como l², con lo cual logramos obtener nuestra primera separación de variables logrando así nuestra primera ecuación diferencial ordinaria:
Del mismo modo tenemos lo siguiente:
en donde se ha introducido una segunda constante, m², para obtener así nuestra segunda ecuación diferencial ordinaria:
Finalmente:
PROBLEMA: Utilícese el método de separación de variables para separar la ecuación diferencial parcial de Helmholtz en tres ecuaciones diferenciales ordinarias mediante el empleo de coordenadas esféricas.
En coordenadas esféricas (r,θ,φ), la ecuación de Helmholtz toma el siguiente aspecto:
Recurriendo al operador Laplaciano tal y como se utiliza cuando hay coordenadas esféricas de por medio, tenemos entonces la siguiente ecuación diferencial parcial de segundo orden:
Nuevamente, y con el propósito de llevar a cabo una separación de variables, escribimos lo siguiente:
con lo cual obtenemos lo siguiente al llevar a cabo las diferenciaciones parciales mostradas:
Del mismo modo:
Substituyendo esto en la ecuación de Helmholtz y dividiendo entre ψ = RΘΦ, tenemos entonces:
Multiplicando por r²senθ y aislando (1/Φ)(d²Φ/dφ²) obtenemos lo siguiente:
Puesto que las tres coordenadas esféricas son independientes la una de las otras, ambos lados (izquierdo y derecho) de esta última relación tienen que ser necesariamente iguales a una constante, la cual podemos escoger como m², con lo cual logramos obtener nuestra primera separación de variables logrando así nuestra primera ecuación diferencial ordinaria:
Del mismo modo:
En el lado izquierdo de la igualdad tenemos únicamente términos en función de R y r, mientras que en el lado derecho de la igualdad tenemos únicamente términos en función de Θ y θ. De nueva cuenta, hemos logrado otra separación de variables. Igualando cada lado a una constante Q, podemos completar de este modo nuestro conjunto de tres ecuaciones diferenciales ordinarias, empezando primero con:
para terminar con:
El método de separación de variables es totalmente válido cuando las variables que están siendo separadas son completamente independientes la una de la otra, o expresado de manera más elegante, cuando las variables son ortogonales. Y puesto que en la descripción de un sistema físico dinámico (a diferencia de un sistema físico estático) la variable del tiempo es independiente de las tres coordenadas espaciales utilizadas en la ubicación tridimensional, podemos tomar una ecuación de onda para separarla de la siguiente manera:
Ψ(p,q,r,t) = P(p)Q(q)R(r)T(t)
Esta, desde luego, es precisamente la forma en la cual obtenemos la ecuación de Schrödinger independiente del tiempo, precisamente mediante el método matemático de separación de variables que nos permite obtener dos ecuaciones diferenciales a partir de una sola, una dependiente del tiempo y la otra independiente del tiempo que es la que hemos estamos manejando aquí.