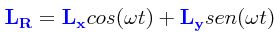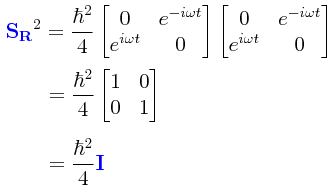La esperanza matemática del cuadrado del momento angular L tendrá un valor específico bien definido para cada valor de l, de modo tal que podemos obtenerla sin mayores problemas:
Por otra parte, para obtener la esperanza matemática de la componente-z del momento angular matricial, o sea Lz = ħJz, debemos tener en cuenta que para cierto valor de j los valores propios eigen de Jz serán diferentes y cubrirán la siguiente gama de valores dando un total de 2j+1 valores distintos:
mj = -j, -j+1, -j+2, -j+3, ... , 0 , ... , j-3, j-2, j-1, j
La esperanza matemática de Jz (y por lo tanto Lz) será el simple promedio aritmético de la suma de todos estos valores, lo cual nos dá:
La esperanza matemática <Jz> siempre será igual a cero porque al momento de tomar la media aritmética siempre habrá tantos valores negativos como positivos de los mj. Sin embargo, y obviamente, la esperanza matemática de la media aritmética cuadrática de Jz ya no será igual a cero porque al ser elevados al cuadrado todos los mj sus signos negativos desaparecen.
PROBLEMA: Demostrar que la esperanza matemática de la media aritmética cuadrática de la componente-z del momento angular, Lz, está dada para cierto valor fijo de l por la siguiente relación:
Utilícense las siguientes dos series en la solución de este problema:
Con el objeto de no estar arrastrando innecesariamente el factor ħ², llevaremos a cabo la demostración apoyándonos en la matriz Jz. Por definición de la esperanza matemática de la media cuadrática de los valores mj, tenemos como punto de partida lo siguiente:
Para cierto valor específico de j, la expansión del numerador nos llevará a lo siguiente:
Tenemos que trabajar en el numerador desarrollándolo y simplificándolo al máximo para saber lo que obtendremos para un valor específico de mj.
Elevando cada binomio al cuadrado (los términos en j² serán identificados en color azul, los términos en j serán identificados en color morado, y los términos numéricos libres de j serán identificados en color rojo):
Hay un total de 2j términos en j², razón por la cual la contribución total numérica al numerador de parte de los términos en j² será:
2j·(j²) = 2j3
Obtener una expresión general para la contribución numérica total de los términos en j es un poco más laborioso, razón por lo cual se presentará el desarrollo intermedio:
Con la ayuda de una de las series dadas arriba, no hay que batallar mucho para dar con la expresión general de la contribución numérica total de los términos en j:
Por último, con la ayuda de otra de las series dadas en el enunciado del problema, podemos ver que la contribución de los términos puramente numéricos al valor numérico total del numerador tiene que ser:
El valor total del numerador será la suma de las tres contribuciones:
Este es el valor numérico del numerador para un valor específico de j. Entonces, finalmente, obtenemos:
Y por extensión, insistiendo en que j = l (así como mj = ml):
PROBLEMA: Obténgase la esperanza matemática <Lz²> para l = 2 de dos maneras distintas: (1) Utilizando la fórmula que se acaba de obtener y, (2) recurriendo directamente a la definición estadística.
(1) Usando la fórmula recién obtenida haciendo l = 2:
(2) Recurriendo directamente a la definición estadística de la esperanza matemática de la media cuadrática:
PROBLEMA: Suponiendo que:
obténgase cada una de estas esperanzas medias cuadráticas.
A continuación se muestra el procedimiento de solución para este problema:
Como puede verse, las esperanzas medias cuadráticas están repartidas en partes iguales en las tres componentes matriciales del momento angular. Esto es cierto antes de que se lleve a cabo una medición sobre un sistema para determinar el valor específico del momento angular a lo largo de cierta componente, la cual usualmente es identificada como la componente-z, lo cual equivale a determinar el valor específico de ml (o lo que es lo mismo, mj). Sin embargo, una vez que se ha llevado a cabo una medición, en virtud de que tenemos ya un solo mj entresacado de entre todos los demás valores posibles restantes sucede una cosa muy curiosa. La esperanza media cuadrática de Lz se vuelve igual a cero. En efecto, de tener una imagen borrosa (en inglés, “fuzzy”) de Lz en la cual todos los valores de mj son igualmente posibles, con el solo hecho de llevar a cabo una medición del sistema hacemos “brincar” al sistema a un estado de momento angular perfectamente definido. En cierta forma, podemos afirmar que la matriz se colapasa pasando de un estado borroso a un estado definido:
Hasta este punto hemos estado utilizando notación matricial compacta para representar todas las matrices relacionadas con el momento angular. Pero no se ha presentado un solo ejemplo específico de alguna de estas matrices, lo cual solventaremos de inmediato.
PROBLEMA: Escríbase la matriz L² para un valor del número cuántico del momento angular l = 2.
Para un número cuántico l = 2 que podemos tomar también como j = 2, habrá un total de 2j+1 = 5 valores distintos de mj, lo cual nos dice que para poder representar a L² tendremos que utilizar una matriz cuadrada de orden 5x5. Pero para un valor dado de j esta matriz tendrá un solo valor eigen que ocupará cada uno de los lugares que corresponden a la diagonal principal, con ceros puestos en el resto de las entradas de la matriz. De este modo:
PROBLEMA: Escríbase la matriz Lz para un valor del número cuántico del momento angular l = j = 2.
A diferencia de la matriz L², la cual posee un solo valor propio eigen para un valor dado de j, la matriz Lz posee un total de 2j+1 valores propios eigen diferentes, y en el caso de j = 2 estos valores serán:
mj = -j, -j+1, -j+2, -j+3, ... , 0 , ... , j-3, j-2, j-1, j
mj = -2, -1, 0, 1, 2
Formamos la matriz Lz poniendo cada uno de estos valores a lo largo de la diagonal principal:
Dado algún valor específico del número cuántico j que corresponda al momento angular, podemos también escribir las matrices que corresponden a los operadores matriciales escalera J+ y J-, y habiendo obtenido estas matrices podemos escribir de inmediato las matrices que corresponden a Jx y a Jy. Para ello, hacemos recurso de las siguientes relaciones:
La forma en la cual se interpretan estas dos relaciones consiste en asignar un valor específico de l y un valor específico de mj como en el siguiente ejemplo en el cual evaluaremos el valor del operador escalera J+ para j = 3 y mj = 1:
El valor del operador escalera J+ para j = 3 y mj = 1 es √10. La pregunta ahora es: ¿en qué lugar dentro de la matriz J+ debemos colocarlo? Esto nos lo fija el delta de Kronecker δab con su propiedad de que cuando sus dos sub-índices a y b son iguales el delta de Kronecker toma el valor de 1, y cuando sus dos sub-índices son desiguales el delta de Kronecker toma el valor de 0. El único valor de m’j para el cual el delta de Kronecker podrá ser diferente de cero en este caso es m’j = 2. De este modo, el valor de debe ser puesto en la matriz cuyo casillero corresponda a las “coordenadas” mj = 1 y m’j = 2. Obviamente, los valores de la matriz no irán colocados a lo largo de la diagonal principal de la matriz.
Sin entrar en tanto detalle, podemos hacer “trampa”con el delta de Kronecker utilizándolo no en su contexto matemático literal que requiere que ambos índices sean rigurosamente iguales para que el delta de Kronecker sea igual a 1, sino en su papel de “ubicador de la posición dentro de la matriz”, haciendo que tome el valor de 1 aunque sus sub-índices no sean matemáticamente idénticos. Esto será útil para ayudarnos en la construcción de la matriz como lo veremos en el siguiente caso.
PROBLEMA: Escríbanse las matrices J+ y J- para un valor del número cuántico del momento angular l = j = 2.
Para un número cuántico l = 2 que podemos tomar también como j = 2, habrá un total de 2j+1 = 5 valores distintos de mj, lo cual nos dice que para poder representar al operador matricial escalera J+ tendremos que utilizar una matriz cuadrada de orden 5x5. La fórmula para obtener los componentes de la matriz J+ cuando j = 2 será la siguiente:
A continuación, haremos que las referencias al valor m’j y al valor mj puestas como sub-índices del delta de Kronecker sean referencias al mismo mj. En pocas palabras, haremos m’j = mj. De este modo, la comilla en el primero tendrá como único propósito el fijar la posición en un renglón específico en la matriz en donde irán siendo colocados cada uno de los elementos que vayan siendo evaluados bajo la raíz cuadrada. Como ya se observó arriba, los únicos elementos de la matriz que no serán cero son los que van puestos a lo largo de la diagonal superior adyacente a la diagonal principal.
A continuación se evaluarán los elementos que van puestos en la matriz J+:
Las entradas en la matriz 5x5 que corresponde a J+ serán las que acabamos de obtener, y cada uno de los deltas de Kronecker nos servirán para fijar la posición de cada entrada dentro de la matriz. Ahora bien, para transcribir los elementos la matriz tenemos una opción. Podemos “ajustar” los sub-índices en los deltas de Kronecker para que correspondan numéricamente a los sub-índices ordinarios con los cuales son identificados los elementos de una matriz convencional:
Afortunadamente, no estamos obligados a respetar al pie de la letra esta convención, y podemos cambiar los sub-índices identificadores si tal cosa sirve a nuestros propósitos. Y en este caso, podemos usar a nuestra conveniencia el hecho de que los sub-índices de los deltas de Kronecker, los cuales son los mismos que los valores de los números enteros que corresponden a los mj, para situarlos ordenadamente en el siguiente arreglo matricial:
De este modo, cada uno de los deltas de Kronecker prácticamente nos “vá diciendo” en dónde podemos colocar cada elemento, obteniendo así la siguiente matriz para J+:
Por otro lado, basta comparar las fórmulas para J+ y J- para darnos cuenta de que la matriz J- será muy parecida a la matriz J+, excepto que sus elementos irán colocados a manera del reflejo de un espejo con respecto a la diagonal principal de la matriz:
Las matrices respectivas L+ y L- se obtienen simplemente multiplicando J+ y J- por ħ.
Teniendo a la mano las matrices J+ y J- para ambos operadores escalera:
podemos obtener de las mismas, para cualquier matriz en particular, las matrices que corresponden a las componentes Jx y Jy del momento angular:
PROBLEMA: Obténganse las matrices Lx y Ly para una matriz que representa un momento angular cuyo número cuántico es j = 2.
Recurriremos a las matrices J+ y J- obtenidas en el problema anterior para un número cuántico j = 2, con las cuales tenemos por un lado:
y por el otro:
Las matrices respectivas Lx y Ly se obtienen simplemente multiplicando Jx y Jy por ħ.
Con lo que hemos visto tenemos suficiente material para resolver lo siguiente:
PROBLEMA: Obténganse las esperanzas matemáticas de las matrices Lx y Ly:
La obtención de estas esperanzas matemáticas para Lx y Ly en realidad equivale a la obtención de las mismas esperanzas matemáticas para Jx y Jy exceptuando el factor multiplicativo ħ. La clave para responder a la pregunta formulada consiste en darse cuenta de que, por la forma en la cual están definidas las matrices J+ y J- en función de las fórmulas dadas arriba, usadas a su vez para definir a las matrices Jx y Jy, las matrices Jx y Jy siempre serán matrices cuya diagonal principal contendrá únicamente ceros, tal y como nos lo confirma el problema anterior resuelto para j = 2. Y la esperanza matemática de cualquier matriz en cuya diagonal aparezcan únicamente ceros será igual a cero. Por lo tanto:
<Lx> = 0___<Ly> = 0
Con lo que hemos visto tenemos suficiente material para intentar darle una explicación física a todo lo que tiene que ver con el análisis matricial del momento angular.
Empecemos por tomar el único valor propio eigen de la matriz L² -que es igual a l(l+1)ħ²- como el cuadrado de una “longitud física” en virtud de que dicha matriz está definida en la forma usual de una longitud evaluada de acuerdo al teorema de Pitágoras en tres dimensiones:
L² = Lx² + Ly² + Lz²
Entonces la raíz cuadrada del eigenvalor será igual al valor que puede tomar la magnitud total del momento angular, lo cual nos permite identificar a esta magnitud de la manera usual como:
|L| = √l(l+1) ħ
De este modo, la Mecánica Matricial nos confirma que el momento angular orbital no tiene un valor único como lo suponía el modelo atómico planetario de Bohr que cuantizaba al momento angular dándole un valor de nħ, y en cambio para un número cuántico principal (en el caso del electrón solitario girando en torno al núcleo del átomo) hay n valores posibles de √l(l+1).ħ
cuyos valores van de 0 a n-1:
l = 0, 1, 2, 3, ... n-1
En el caso particular de n =1, o sea el menor valor de energía, el valor de l es cero y por lo tanto la magnitud |L| del momento angular orbital también es cero. Este es un resultado importante porque marca una diferencia de fondo entre la Mecánica Matricial y el modelo atómico planetario de Bohr. Recuérdese que en el modelo de Bohr el momento angular está cuantizado de acuerdo con la relación L = nħ, y puesto que n = 1 para el estado basal en el modelo de Bohr esto significa que en la primera órbita (el estado energético más bajo) el electrón tiene un momento angular orbital igual a ħ. Pero en la Mecánica Matricial el momento angular orbital no tiene un valor de ħ, es cero. Y no sólo esto, sino que mientras que en el modelo de Bohr el electrón en el estado basal está dándole vueltas al núcleo a una distancia constante exactamente igual a a0 (el radio de Bohr), en la Mecánica Matricial este radio desaparece en nuestras manos quedándonos tan sólo una probabilidad de que el electrón esté situado a cierta distancia (variable) del átomo, siendo el radio de la supuesta órbita de los electrones en los átomos de Bohr algo considerado como inobservable, aunque con la mayor probabilidad de encontrar al electrón precisamente a la distancia a0, más no la certeza. De este modo, de la imagen que teníamos del modelo atómico planetario de Bohr con una órbita fija y con un momento angular igual a ħ:
emerge en su lugar la imagen de un electrón con una localización imposible de ser especificada con exactitud, una imagen borrosa, difusa:
y si pudiésemos tener en este momento una gráfica de una distribución de probabilidad P(r) dándonos la probabilidad de encontrar al electrón a cierta distancia del núcleo del átomo (en este tipo de gráficas la probabilidad se mide no por la altura de la ordenada en la gráfica sino por el área debajo de la curva situada entre dos distancias r1 y r2), lo más seguro es que tendríamos algo como lo siguiente confirmándonos que la concha esférica en donde hay una mayor probabilidad de encontrar al electrón en el estado basal estaría situada a una distancia a0, o sea la primera órbita del radio de Bohr, en donde la gráfica de la distribución de probabilidad debe adquirir su mayor altura:
Supóngase ahora que introducimos un átomo de un solo electrón en un campo magnético externo cuya dirección hacemos coincidir con el eje-z. El análisis matricial nos ha demostrado que la dirección del vector momento angular orbital L no puede ser arbitraria, y éste vector L estará orientado de tal manera que la componente Lz en la dirección del eje-z, estará cuantizada con valores discretos:
Lz = mlħ
en donde ml es el número cuántico denominado como el número cuántico magnético cuyos valores enteros posibles varían desde -l hasta +l:
ml = -l, -l +1, -l +2, -l + 3, ... , l - 3, l - 2, l - 1, l
Destaca el hecho de que para un l dado el valor máximo de Lz (= lħ) siempre será menor que |L| = √l(l+1) ħ.
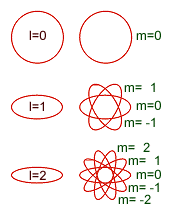
Tal vez la manera más sencilla de recordar la relación que existe entre el número cuántico ml, al cual muchas veces se le simboliza simplemente como m, y el número cuántico l, sea con la ayuda del siguiente “diagrama de puntos”:
Antes del advenimiento de la Mecánica Matricial, Sommerfeld había logrado dar una explicación un poco forzada a “esas líneas adicionales que aparecen en el espectro del hidrógeno cuando se aplica un campo magnético a la muestra bajo observación” invocando efectos relativistas que el modelo atómico planetario de Bohr no había tomado en cuenta, introduciendo artificialmente de este modo un momento angular orbital en el modelo de Bohr. Visualmente se imaginaban las líneas adicionales en el espectro del hidrógeno (bajo la aplicación de un campo magnético) como el reflejo de órbitas excéntricas diferentes a las órbitas perfectamente circulares del modelo de Bohr:
Como hemos visto, el modelo matricial no sólo no invoca efecto relativista alguno, sino que ni siquiera dá credibilidad alguna a las órbitas perfectamente circulares del modelo de Bohr que confinan al movimiento del electrón a un plano, mucho menos a órbitas excéntricas, considerando tales órbitas como no observables. En lugar de ello, se introduce una incertidumbre en casi todo lo que ocurre en el mundo sub-microscópico que termina por sepultar de manera definitiva el muy mecanístico modelo atómico planetario de Bohr, una incertidumbre que nos presenta a la ubicación del electrón en torno al núcleo del átomo como una imagen esférica borrosa.
En la nueva visión vectorial que nos proporciona la Mecánica Matricial sobre el momento angular, para un número cuántico l = 1 tenemos el siguiente panorama:
Asimismo, para un número cuántico l = 2, el bosquejo vectorial será el siguiente:
No es difícil construír un diagrama como el que se acaba de mostrar observando que la longitud del vector L tiene un valor constante, lo cual nos fija el radio del círculo punteado que vemos arriba, y observando que a lo largo del eje-z las proyecciones del vector L sobre dicho eje deben estar igualmente espaciadas a la misma distancia.
Desde antes de que la Mecánica Matricial explicara el desdoblamiento de las líneas del espectro al aplicársele a la muestra un campo magnético, ya en 1896 el físico holandés Pieter Zeeman había descubierto experimentalmente tal fenómeno, hoy conocido como el efecto Zeeman. En este experimento se coloca una muestra en ausencia de un campo magnético externo, y se observa que en presencia de un campo externo cada línea se desdobla en un número de líneas diferentes, y el cambio que se observa en la frecuencia de las líneas es directamente proporcional a la magnitud del campo magnético aplicado. La observación de líneas espectrales adicionales significa que un átomo posee niveles discretos adicionales de energía cuando se le introduce en un campo magnético externo. (Una visión un poco más moderna del efecto Zeeman así como de otros efectos de naturaleza cuántica los explica en términos del rompimiento de la simetría. En el caso del efecto Zeeman, cuando no hay campo magnético aplicado a la muestra no hay preferencia espacial alguna de ningún tipo, habiendo una simetría espacial tridimensional plena. Al aplicarse un campo magnético, puesto que las líneas de este campo magnético poseeen cierta dirección la simetría espacial se rompe y el efecto Zeeman debido a los momentos angulares diferentes sale a relucir).
Puesto que para l = 1 hay tres valores posibles que puede tomar el momento angular orbital (-ħ, 0 y +ħ), y puesto que para l = 2 hay seis valores posibles (-2ħ, -ħ, 0, ħ y 2ħ) que puede tomar el momento angular orbital, el espectro producido por la emisión de un fotón al caer del estado n =2 al estado n = 1 que consiste de una sola línea en ausencia de un campo magnético se convertirá en un espectro de nueve líneas como podemos verlo a continuación:
Para poder ponerle algunos números al asunto, es necesario considerar primer a un electrón que se mueve en una trayectoria circular, produciendo una corriente eléctrica que será igual a la carga del electrón multiplicada por el número de veces que pasa el electrón por un mismo punto:
I = ef
siendo f la frecuencia de rotación del electrón. La espira circular de corriente produce a su vez un campo magnético parecido al de un pequeño imán, y podemos considerar que existe un momento de dipolo magnético μ asociado con el electrón que está orbitando que es igual a la corriente eléctrica equivalente multiplicada por el área encerrada por la órbita circular (vectorialmente hablando, este momento de dipolo magnético apunta en una dirección inversa a la dirección del momento angular en virtud de ser la carga del electrón una carga negativa):
|μ| = IA = (ef)(πr²)
De la definición clásica del momento angular, tenemos entonces que:
Vectorialmente, indicando que el vector momento de dipolo magnético μ y el vector momento angular L apuntan en direcciones contrarias:
Si la espira de corriente se coloca en presencia de un campo magnético externo B, clásicamente experimentará un torque τ que tiende a alinear al momento de dipolo magnético μ con el campo B:
τ = μ×B
De este modo, el sistema tiene una energía potencial EB cuyo cambio dá el trabajo hecho por el torque τ cuando varía la orientación de μ. De este modo, de la expresión vectorial para el torque podemos demostrar que:
EB = - μ·B
Haciendo coincidir la dirección del campo magnético B con la dirección del eje-z y utilizando lo anterior obtenemos entonces:
Puesto que Lz = mlħ, esto significa que la energía total estará dada por la siguiente relación:
siendo la energía cuantizada antes de que sea aplicado el campo magnético. De este modo, en presencia del campo magnético cada nivel de energía E0 se desdoblará en 2l+1 subniveles igualmente separados. El factor eħ/2m es conocido como el magnetón de Bohr.
PROBLEMA: Calcúlense los momentos magnéticos posibles para un nivel de energía n = 3: (1) de acuerdo al modelo atómico planetario de Bohr, y (2) de acuerdo a la Mecánica Matricial.
(1) De acuerdo al modelo atómico planetario de Bohr en la que el momento angular orbital del electrón está cuantizado de acuerdo a la relación L = nħ, para n = 3 sólo hay un momento magnético posible, siendo éste:
que es igual a tres tantos del magnetón de Bohr, o sea:
μB = 3(0.927×10-23 joules/Tesla)
μB = 2.78×10-23 joules/Tesla
μB = 2.78×10-23 joules/Tesla
(2) De acuerdo a la Mecánica Matricial, para n = 3 hay tres valores posibles de l, 0, 1 y 2.
Para l = 0, L= √l(l+1) ħ = 0 y entonces μB = 0.
Para l = 1, L = √l(l+1) ħ = √1(1+1) ħ = √2 ħ y entonces:
μB = √2(0.927×10-23 joules/Tesla) = 1.31×10-23 joules/Tesla
Para l = 2, L = √l(l+1) ħ = √2(2+1) ħ = √6 ħ y entonces:
μB = √6(0.927×10-23 joules/Tesla) = 2.27×10-23 joules/Tesla
PROBLEMA: Si se tiene un átomo de helio ionizado, determínese su momento magnético debido al movimiento orbital del electrón solitario si dicho electrón se encuentra en una órbita n = 2: (1) de acuerdo al modelo atómico planetario de Bohr, y (2) de acuerdo a la Mecánica Matricial.
(1) De acuerdo a la teoría de Bohr en la que el momento angular orbital del electrón está cuantizado de acuerdo a la relación L = nħ, para n = 2 sólo hay un momento magnético posible, siendo éste:
μB = (e/2m) L = (e/2m) nħ = n(eħ /2m)
μB = (2)(0.927×10-23 joules/Tesla)
μB = 1.854×10-23 joules/Tesla
μB = (2)(0.927×10-23 joules/Tesla)
μB = 1.854×10-23 joules/Tesla
(2) De acuerdo a la Mecánica Matricial, para n = 2 habrá dos valores posibles de l, l = 1 y l = 2. Entonces:
μB = (e/2m)L = (e/2m)√l(l+1) ħ = (eħ/2m)√l(l+1)
μB = (0.927×10-23 joules/Tesla)√1(1 + 1)
μB = 1.31×10-23 joules/Tesla__para l = 1
μB = (0.927×10-23 joules/Tesla)√1(1 + 1)
μB = 1.31×10-23 joules/Tesla__para l = 1
μB = 0__para l = 0
PROBLEMA: Encuéntrese una expresión para el desdoblamiento de una línea que sea ocasionado por el efecto normal de Zeeman.
La energía del fotón emitido o absorbido está dada por la relación E = hf = hc/λ. Diferenciando esta expresión con respecto a λ se tiene lo siguiente:
Pero el cambio en energía será igual a ΔEB = (eħ/2m)B. Entonces:
Esta fórmula, tal y como está dada, contiene en el numerador a la constante reducida de Planck y en el denominador a la constante ordinaria de Planck. Sin embargo, no es conveniente simplificarla aún más porque para efectos de cálculos numéricos se tiene en el numerador al magnetón de Bohr y en el denominador a una constante física muy conocida cuyo valor es hc = 12.4×103 eV·Å.
PROBLEMA: ¿Cuál será la separación normal de Zeeman en la línea del mercurio de 4916 Å cuando se le sumerge en un campo magnético igual a 0.6 Tesla?
Este problema consiste en la aplicación directa de la fórmula obtenida arriba:
Δλ = {[λ²(eħ/2m)]/hc} B
Δλ = {[(4916 Å)²(5.79×10-5 eV/Tesla)]/(12.4×103 eV·Å)} (0.6 Tesla)
Δλ = 0.0676 Å
Δλ = {[(4916 Å)²(5.79×10-5 eV/Tesla)]/(12.4×103 eV·Å)} (0.6 Tesla)
Δλ = 0.0676 Å
PROBLEMA: Para una radiación emitida por una muestra a la cual se le mide una longitud de onda igual a 4500 Å al serle aplicado un campo magnético de 0.3 Tesla, ¿cuál será la separación normal de Zeeman que podemos esperar entre dos líneas adyacentes?
Nuevamente, utilizamos la fórmula obtenida arriba:
Δλ = {[λ²(eħ/2m)]/hc} B
Δλ = {[(4500 Å)²(5.79×10-5 eV/Tesla)]/(12.4×103 eV·Å)} (0.3 Tesla)
Δλ = 2.84×10-2 Å
Δλ = {[(4500 Å)²(5.79×10-5 eV/Tesla)]/(12.4×103 eV·Å)} (0.3 Tesla)
Δλ = 2.84×10-2 Å
PROBLEMA: Supóngase que una línea de 5000 Å muestra una separación normal de Zeeman entre líneas adyacentes de 0.001 Å. Determínese la magnitud del campo magnético que le está siendo aplicado a la muestra.
De:
Δλ = {[λ²(eħ/2m)]/hc} B
obtenemos:
B = (hcΔλ)/[λ²(eħ/2m)]
Metiendo números:
B = [(12.4×103 eV·Å)(10-3 Å)]/[(5×103 Å)²(5.79×10-5 eV/Tesla)]
B = 8.57×10-3 Tesla
B = 8.57×10-3 Tesla
Nos queda un cabo suelto por atar. Es un hecho bien conocido para quienes alguna ocasión en su vida han jugado con un trompo el que cuando el trompo está girando alrededor de su eje de simetría entonces al formar un ángulo con la vertical el trompo no cae al suelo por la acción de la fuerza de la gravedad sino que inicia un movimiento de rotación en torno a la vertical oponiéndose a la caída, un movimiento de rotación conocido como precesión el cual es activado por el torque τ (resultante del producto vectorial de la fuerza de la gravedad Fg por el brazo de palanca) y en respuesta al cual el trompo inicia la precesión como consecuencia inevitable del principio de la conservación del momento angular L:
El físico irlandés Joseph Larmor propuso que a escalas sub-microscópicas los electrones en rotación al ser objeto de una fuerza provocada por un campo magnético externo también debían exhibir un efecto de precesión, hoy conocido como la precesión de Larmor:
lo cual debe ser un hecho en virtud de que el momento magnético μ de un electrón sumergido en un campo magnético externo B también debe experimentar un torque τ dado por (el signo negativo proviene de la carga negativa del electrón):
τ = μ×B = - (e/2m)L×B
Este torque producirá un cambio en el momento angular L dado por:
τ = dL/dt
con lo cual:
dL/dt = - (e/2m)L×B
El cambio infinitesimal dL en L es perpendicular al vector momento angular L y al vector campo magnético B, dando como resultado una precesión de L alrededor de B. Suponiendo que este efecto que es válido clásicamente sea también válido en el mundo sub-microscópico, entonces de la siguiente figura (en la cual el vector momento magnético μ del electrón apunta en dirección contraria a la dirección del vector momento angular L del electrón a causa del signo negativo de la carga eléctrica del electrón):
y de la siguiente figura:
tenemos que:
dφ = |dL|/Lsen(θ)
lo cual nos dá como la frecuencia angular precesional ωp lo siguiente:
ωp = dφ/dt = |dL/dt|/[Lsen(θ)]
ωp = {(e/2m)LBsen(θ)}/Lsen(θ)
ωp = (e/2m)B
ωp = {(e/2m)LBsen(θ)}/Lsen(θ)
ωp = (e/2m)B
siendo ωp igual a la diferencia de frecuencia angular observada en el efecto Zeeman normal.
Tomando en cuenta la precesión de Larmor, entonces la imagen que se nos viene a la mente del momento angular de una partícula atómica o sub-atómica es la de una partícula cuya componente Lz del momento angular adquiere cierto valor definido (entresacado de entre varios valores posibles con igual probabilidad todos ellos de ser sacados) después de haberse llevado a cabo una medición, y cuya “magnitud” invariable L² (reflejada en su autovalor √l(l+1) (que es lo que venimos detectando a fin de cuentas en el laboratorio) es un vector que está girando en torno al eje-z describiendo lo que parece ser un cono. Es de aquí de donde nos viene la imagen del vector momento angular con una componente Lz constante y con componentes Lx y Ly que varían alternadamente describiendo un círculo en torno al eje-z dando así origen a la precesión de Larmor.
Estableciendo una analogía con la fórmula clásica que nos describe a un vector radial r de longitud fija girando en torno a un punto central:
r = x cos(ωt) + y sen(ωt)
de la cual obtenemos un círculo de radio constante:
r² = x² + y²
podemos intentar postular un operador matricial LR que nos describa un efecto similar, un operador de momento angular tal y como:
Para el momento angular del spin del electrón, lo anterior puede escribirse como:
Familiarizados con las matrices que nos definen a Sx y a Sy, esto último puede ser sometido a la siguiente simplificación:
A estas alturas, cabe formularse una pregunta: ¿permanecerá constante SR² al igual que como r² también permanece constante en la fórmula clásica? Esto puede verificarse de inmediato de la siguiente manera:
Efectivamente, SR² permanece constante todo el tiempo, aunque Sx y Sy estén variando continuamente.
PROBLEMA: Obténganse las siguientes esperanzas matemáticas que corresponden a la componente matricial Sx del spin del electrón:
Puesto que los valores propios eigen de la matriz Sx son:
λ1 = - ħ/2____λ2 = + ħ/2
la evaluación de las esperanzas matemáticas pedidas resulta directa:
Más aún, puesto que las otras dos matrices Sy y Sz también tienen los mismos valores eigen que Sx, las esperanzas matemáticas que hemos evaluado para el eje-x serán las mismas que las que correspondan al eje-y y al eje-z.
En virtud de que la incertidumbre sobre los autovalores eigen representados por una matriz A está dada por:
entonces las incertidumbre en los valores de las matrices Sx, Sy y Sz serán las siguientes y, antes de que se lleve a cabo una medición, todas serán iguales:
Una vez que se lleva a cabo una medición para determinar el valor que corresponda a la componente matricial del momento angular en el eje-z, la incertidumbre en la componente-z se desvanece, pero las incertidumbres en las dos componentes restantes persiste. La única manera en la cual podemos tomar conocimiento de la componente en el eje-x será llevando a cabo una medición del momento angular sobre el eje-x. Pero al hacerlo destruímos la información previa que teníamos sobre la componente del eje-z. En tal caso, habrá incertidumbres en las componentes del eje-y y del eje-z repartidas en partes iguales. No hay manera de esquivar esta consecuencia inevitable de la Mecánica Matricial: al llevar a cabo alguna medición sobre observables incompatibles, cualquier conocimiento que adquiramos sobre una observable destruirá el conocimiento previo que hayamos adquirido sobre las otras observables.
Agregaremos por último que la simetría espacial no sólo se puede romper con un campo magnético. También se puede romper con un campo eléctrico que estará orientado en cierta dirección específica (polarizado), con lo cual también podemos esperar también que se produzca un desdoblamiento de líneas. Este efecto fue observado por vez primera por el físico alemán Johannes Stark quien lo descubrió experimentalmente en 1913 antes del advenimiento de la Mecánica Cuántica, y es conocido como el efecto Stark.