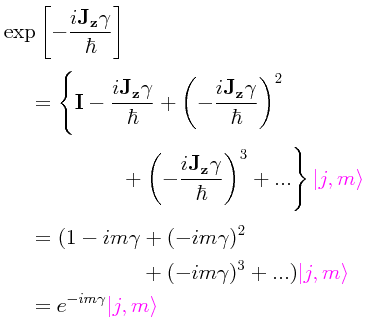El grupo de rotaciones ortogonales O(3) (también simbolizado como O3+ en la literatura)
La forma más directa de comenzar un estudio de las rotaciones en el espacio tridimensional consiste en especificar un eje de rotación y el ángulo de rotación. Se requiere un mínimo de tres números para poder caracterizar una rotación general: los ángulos polar β y azimutal α de un vector n tomados en la dirección del eje de rotación, y el ángulo de rotación θ. Ya se vió en las dos entradas “Operadores de rotación” que esta es una manera de hacerlo. Otra forma completamente equivalente de especificar la misma rotación consiste en especificar las tres componentes rectangulares Cartesianas del vector nθ. Sin embargo, estas maneras de especificar rotaciones no son las más convenientes desde el punto de vista del estudio de las propiedades de grupo de las rotaciones, ya que por principio de cuentas a menos de que el ángulo θ sea un ángulo infinitesimal o de que el vector unitario n siempre esté apuntando en la misma dirección, no es posible sumar vectores de la forma nθ para caracterizar una sucesión de rotaciones consecutivas. Resulta mucho más fácil trabajar con una matriz ortogonal 3×3 R porque de este modo el efecto de rotaciones sucesivas se puede obtener simplemente multiplicando las matrices ortogonales apropiadas.
El grupo de matrices ortogonales 3×3 recibe la simbolización técnica de grupo O(3), en donde la O es la alusión directa a que se trata de un grupo cuyos elementos son Ortogonales, y el número 3 indica que las matrices serán las apropiadas para las rotaciones que se llevan a cabo en un espacio de tres dimensiones. Una notación alterna, un poco más específica y también de amplio uso, es la designación O3+, en donde el signo + usado como super-índice indica que las matrices en las que estamos interesados son aquellas para las cuales su determinante es +1, ya que en caso contrario de que su determinante sea -1 el efecto que producen es el de una reflexión y no el de una rotación.
Las matrices ortogonales, cualesquiera que sea su tamaño, deben cumplir con la condición esencial de que la transpuesta de la matriz debe ser igual a la inversa de la matriz:
RT = R-1
lo cual es equivalente a la condición:
RT · R = R · RT = I
siendo I la matriz identidad. Aunque en el caso de una matriz ortogonal 3×3 esta matriz consta de 9 entradas, la condición de ortogonalidad reduce esto a 6 ecuaciones independientes en virtud de que siendo el producto matricial R·RT igual al producto matricial RT·R, la matriz ortogonal resulta ser una matriz simétrica con 6 entradas independientes. Como resultado de esto, hay 9-6.=.3 números independientes en R, lo mismo que se obtuvo previamente por métodos más elementales.
Las matrices ortogonales forman un grupo bajo la operación de multiplicación al cumplir con los cuatro requerimientos básicos para que se les clasifique como un grupo:
1) El producto de dos matrices ortogonales es igual a una matriz ortogonal ya que (usando el resultado matemático de que la transpuesta del producto de dos matrices es igual al producto de las transpuestas de las matrices tomado en el orden inverso):
(R1·R2)(R1·R2)T = R1·R2·R2T·R1T
(R1·R2)(R1·R2)T = R1·R2·R2-1·R1-1
(R1·R2)(R1·R2)T = R1·I·R1-1
(R1·R2)(R1·R2)T = I
2) La propiedad asociativa se cumple por el hecho de que, siendo matrices los elementos del grupo, se hereda la propiedad asociativa que es válida para cualquier matriz:
R1·(R2·R3) = (R1·R2)·R3
3) La matriz identidad I que corresponde físicamente a ninguna rotación es heredada también de las mismas características del conjunto general de matrices:
R·I = I·R = R
4) La matriz inversa R-1 que corresponde a una rotación ortogonal en el sentido opuesto a la rotación que produce el elemento R también forma parte de los elementos del grupo ya que produce el elemento identidad I:
R·R-1 = R-1·R = I
Hablando en términos generales, no todas las matrices forman un grupo, ya que hay matrices cuadradas conocidas matrices singulares para las cuales no existe un elemento inverso con el cual al ser multiplicadas se obtenga la matriz identidad. La principal característica de las matrices singulares es que son matrices cuyo determinante es igual a cero, lo cual excluye de inmediato la posibilidad de que puedan tener un inverso. Pero si del universo posible de todas las matrices cuadradas tomamos únicamente aquellas matrices que poseen un elemento inverso y dejamos fuera del conjunto a las matrices singulares, entonces tenemos ya un conjunto general de matrices que puede ser clasificado como un grupo. Sin embargo, no todas las matrices que pertenecen a este gran grupo son matrices ortogonales, ya que hay matrices que tienen un elemento inverso pero las cuales al ser multiplicadas por su transpuesta no producen la matriz identidad. Pero si de este gran grupo de matrices tomamos un subgrupo que contenga a todas aquellas matrices cuadradas que cumplan con la condición de ortogonalidad, entonces se tiene el subgrupo ortogonal que podemos tomar como el grupo ortogonal con el que usualmente trabajamos. En este procedimiento de exclusión sucesiva, puede verse cómo de un conjunto infinitamente grande de elementos se va tomando un subconjunto cada vez más restringido hasta obtener aquél subconjunto que cumpla con las restricciones que le estamos imponiendo. Pero no hay que perder de vista el hecho de que hay propiedades generales del “gran grupo” que van siendo heredadas sucesivamente a los subgrupos cada vez más restringidos que vamos formando, como lo es el caso de la propiedad asociativa que se mantiene firme para todo el gran conjunto de todas las matrices cuadradas posibles así como para todos los subgrupos que vayamos formando a partir del gran grupo.
Puesto que algunas de las propiedades encontradas en el grupo de rotaciones ortogonales son compartidas por otros grupos mecánico-cuánticos, vale la pena hacer un repaso de tales propiedades, entre las cuales encontramos el hecho de que una matriz cualquiera que represente una rotación pura (esto es, que deja sin cambio alguno la longitud de un vector que sea girado por aplicación sobre el mismo de dicha matriz de rotación) tiene las características de que, si consideramos a dicha matriz formada por vectores columna (en el caso de una matriz 5×5, esta puede ser sub-dividida en cinco vectores columna):
(1) Cada uno de los vectores columna tiene una longitud igual a la unidad.
(2) Los vectores columna son perpendiculares el uno al otro (el producto vectorial punto de ambos es igual a cero).
Estos dos requisitos se pueden resumir en un solo enunciado diciendo que los vectores columna son ortogonales.
Si además de tener vectores columna que son ortogonales, el determinante de la matriz es igual a +1, la matriz representa una rotación pura. El caso para el cual el determinante de la matriz es igual a -1 queda excluído porque una matriz así lo que produce es una reflexión y no una rotación pura.
PROBLEMA: Demuéstrese que la siguiente matriz:
representa una rotación pura.
Considerando a la matriz T formada por dos vectores columna T1 y T2:
se tiene que la longitud del vector columna T1 es:
mientras que la longitud del vector columna T2 es:
El producto punto T1·T2 de los dos vectores columna es:
Los resultados obtenidos indican que los vectores T1 y T2 son ortogonales:
Por otro lado, el determinante de la matriz T es:
Se concluye que la matriz T representa una rotación pura en el espacio de dos dimensiones.
Usando el mismo procedimiento, resulta fácil verificar que las siguientes matrices A y B también representan rotaciones puras:
PROBLEMA: Demuéstrese que la siguiente matriz de rotación:
representa una rotación pura. Asimismo, obténgase el inverso de este operador matricial de rotación.
Las tres columnas de la matriz de rotación obviamente son linealmente independientes, como en el caso de la primera columna C1 y la segunda columna C2:
Y cualquiera de las tres columnas, multiplicada por sí misma, nos produce la unidad, como en el caso de la segunda columna:
Por otro lado, se verifica fácilmente que el determinante de la matriz ortogonal de rotación es igual a la unidad. Por lo tanto, la matriz constituye una rotacion pura.
Para obtener la matriz inversa de la matriz ortogonal de rotación proporcionada, podemos proceder por la vía ardua multiplicando dicha matriz por otra matriz cuyos nueve elementos desconocidos serán determinados en un sistema de nueve ecuaciones lineales con nueve incógnitas tras igualar el producto con la matriz identidad. O podemos proceder por el camino fácil sabiendo de antemano que el operador matricial inverso es aquél que invierte el sentido de la rotación en una magnitud θ, o sea, una rotación igual a -θ:
Entonces la matriz de rotación inversa a la matriz ortogonal de rotación tiene que ser:
El grupo unitario unimodular SU(2)
El conjunto de matrices unitarias n×n, para las cuales se cumple la condición de unitariedad bajo la cual para cualquier matriz U que corresponda a dicho grupo el producto de la matriz U por su transconjugado U† (el conjugado complejo de la transpuesta de la matriz) produce la matriz identidad I, forma un grupo. Esto conduce a la definición del grupo de rotaciones unitarias U(n) en donde el número n especifica la dimensión del espacio bajo consideración, y el cual incluye todas las rotaciones que se pueden simbolizar a través de matrices unitarias. Obviamente, U(n) es un grupo al cumplirse todas las condiciones para clasificarlo como tal, ya que existe en el grupo el elemento identidad I, y todo elemento U del grupo tiene su elemento inverso U-1 que es U†. La propiedad asociativa se cumple automáticamente por tratarse de matrices para las cuales se cumple dicha propiedad.
Si se impone la restricción adicional de que el determinante de las matrices unitarias sea igual a +1, cada subgrupo dentro del grupo de rotaciones U(n) recibe el nombre de subgrupo especial SU(n) o grupo unitario unimodular. Para n.=.2 se tiene el grupo SU(2), en donde el elemento general del grupo se define de la siguiente manera:
en donde a y b son números complejos que satisfacen la condición unimodular:
El elemento inverso es:
La verificación de que la matriz U que se ha definido arriba es una matriz unitaria se lleva a cabo de manera directa usando para ello la condición unimodular:
La relación de cerradura de acuerdo a la cual el producto de dos elementos de un grupo debe producir otro elemento del mismo grupo que cumpla con las mismas condiciones que satisfacen los demás elementos del grupo (esto implica que el elemento que resulte de un producto debe ser también una matriz unitaria unimodular) se puede satisfacer de la siguiente manera:
siendo la condición para la matriz unitaria unimodular resultante:
Los números complejos a y b usados para definir el grupo unitario unimodular SU(2) son conocidos como los parámetros Cayley-Klein. Aunque no parezca obvio a primera vista que el grupo unitario unimodular SU(2) sea capaz de llevar a cabo rotaciones, históricamente hablando la conexión entre la matriz unitaria unimodular y una rotación en el espacio fue descubierta desde mucho antes del advenimiento de la Mecánica Cuántica, a grado tal que los parámetros Cayley-Klein han sido utilizados para describir movimientos complicados de giróscopos en la cinemática de los cuerpos rígidos. Y aunque no parezca obvio tampoco a primera vista que un grupo de rotación definido mediante matrices de tamaño 2×2 sea capaz de llevar a cabo rotaciones en un espacio Euclideano de tres dimensiones expecificadas en tres ejes (x,y,z), recuérdese cómo al desarrollar operadores de rotación para partículas de spin 1/2 en la entrada “Operadores de rotación II” fue posible utilizar las tres matrices 2×2 de Pauli para obtener tales operadores de rotación capaces de efectuar rotaciones en un espacio tridimensional. De hecho, podemos escribir como una matriz unitaria unimodular U(a,b) a la matriz 2×2 que caracteriza a un sistema físico de spin 1/2:
si establecemos las siguientes comparaciones entre las partes reales e imaginarias de los componentes respectivos de ambas matrices:
PROBLEMA: Demuéstrese que la siguiente matriz:
en donde σ es un vector de matrices de Pauli y a.=.(a1,a2,a3) , es una matriz unimodular.
Para demostrar que la matriz en cuestión es una matriz unimodular, el primer paso consiste en demostrar que es una matriz unitaria. Para ello, simbolícese el numerador como:
La transconjugada de esto resulta ser precisamente lo que se tiene en el denominador:
Reescribimos ahora a la matriz M de la siguiente manera tipográficamente correcta (estrictamente hablando, el cociente de dos matrices no es una operación que esté matemáticamente definida, y para que la matriz M tenga sentido se vuelve necesario darle el siguiente significado que es el más común):
El transconjugado de esto es:
De este modo, el producto de la matriz M por su transconjugado (producto que debe resultar igual a la matriz identidad si es que la matriz M realmente es una matriz unitaria) es:
Para poder simplificar esto último, por otro lado se tiene:
De este modo se obtiene:
Por lo tanto:
Se concluye que la matriz M es una matriz unitaria.
Para demostrar que la matriz es unimodular, se tiene que verificar que el determinante de la misma sea igual a +1. Para este efecto, se tiene que:
Usando la propiedad de que el determinante de un producto de matrices es igual al producto de los determinantes de las matrices, se tiene:
De esto último se tiene también que:
Entonces:
Puesto que el determinante de la matriz unitaria M es igual a +1, se concluye que la matriz es unimodular.
Se puede definir una matriz unitaria unimodular aún más general agregando como factor multiplicativo un factor de fase (aunque como ya se ha dicho antes, los factores de fase carecen de relevancia física) en la manera que se muestra a continuación:
El grupo de rotaciones de Euler
Uno de los grupos de operadores de rotación más importantes dentro de la Mecánica Cuántica, históricamente hablando, es el que está basado en los ángulos de Euler (α,β,γ), los cuales fueron introducidos en la entrada titulada “Los grupos de rotación II”.
Detrás de las rotaciones descritas mediante los ángulos de Euler, subyace un teorema básico conocido como el Teorema de Rotación de Euler demostrado por Leonhard Euler en 1775 recurriendo a argumentos geométricos elementales, y el cual afirma lo siguiente: en el espacio tridimensional, cualquier desplazamiento de un cuerpo rígido tal que algún cierto punto en el cuerpo rígido permanezca fijo en la misma posición, es equivalente a una rotación sencilla en torno a cierto eje que pase a través del punto fijo. Esto implica que la composición de dos rotaciones es equivalente a una rotación, e implica a su vez que la descripción de las rotaciones mediante ángulos de Euler satisface lo que se requiere para poder construír un nuevo grupo de rotaciones conocido como el grupo de rotaciones de Euler.
Convencionalmente, las rotaciones usadas para definir a los ángulos de Euler están esquematizadas en un diagrama como el siguiente (la línea verde es conocida como la línea de nodos, formada por la intersección entre el plano-xy que es el plano original y el plano XY que es el plano final):
Las rotaciones de Euler se llevan a cabo usando una secuencia de tres pasos. En el primer paso el cuerpo rígido es girado en un sentido contrario al sentido en el que giran las manecillas de un reloj mecánico (como se ve desde el lado positivo del eje-z) en torno al eje-z en un ángulo α. Imaginemos ahora que se tiene un eje-y incrustado (por así decirlo) en el cuerpo rígido de tal forma que antes de llevarse a cabo la rotación en torno al eje-z el eje-y del cuerpo rígido coincide con el eje-y usual al cual llamaremos eje-y fijo en el espacio. Como puede verse en la figura de arriba, después de llevarse a cabo la primera rotación, el eje-y del cuerpo rígido ya no coincide con el eje-y fijo en el espacio. Para mayor claridad en la distinción, podemos simbolizar al nuevo eje-y como eje-y’. Tras esto, el segundo paso consiste en llevar a cabo una rotación en torno al eje-y’ en un ángulo β. Como resultado, el eje-z en el cuerpo rígido ya no coincide con la dirección del eje-z fijo en el espacio. Para mayor claridad en la distinción, podemos simbolizar al nuevo eje-z como eje-z’. El tercer paso final consiste en llevar a cabo una rotación en torno al eje-z’ en un ángulo γ. Como resultado, el eje-y’ del cuerpo rígido se convierte en el eje-y’’ que en la figura de arriba está simbolizado como el eje-Y final.
En términos de matrices ortogonales 3×3, el producto de las tres operaciones de rotación llevadas a cabo con ángulos de Euler se puede escribir como (obsérvese que el orden seguido es de derecha a izquierda puesto que éste es el orden con el cual cada operación de rotación se va aplicando a aquello sobre lo cual actuará la rotación combinada):
Cabe formular aquí una nota precautoria. Muchos libros de mecánica clásica prefieren llevar a cabo la segunda rotación (la rotación intermedia, la que se lleva a cabo en el segundo paso) en torno al eje-x del cuerpo rígido en lugar de llevarla a cabo en torno al eje-y del cuerpo rígido. Sin embargo, esta convención propia de la mecánica clásica resulta inconveniente y es usualmente evitada en la Mecánica Cuántica en virtud de que al llevarse a cabo la rotación intermedia con un operador matricial exponencial que contiene en el exponente (como factor) el número imaginario i, la matriz de Pauli para el eje-y al tener como entradas números imaginarios termina produciendo como resultado de la multiplicación con i una matriz con entradas reales a las cuales resulta más fácil darles interpretación física (se verá esto en mayor detalle más abajo).
En la expresión que se ha escrito arriba para la rotación R(α,β,γ) aparecen Ry' y Rz', las cuales son matrices en torno a ejes anclados al cuerpo rígido. Este tipo de acercamiento a las rotaciones de Euler resulta algo inconveniente en la Mecánica Cuántica al haberse obtenido previamente en otras entradas expresiones sencillas para los componentes fijos en el espacio (sin las comillas como super-índices) del operador mecánico-cuántico del momento angular S pero no para las componentes de los ejes que correspondan a un cuerpo rígido. Y pensándolo bien, una función de onda no es un cuerpo rígido (aunque ello no presenta obstáculo alguno para llevar a cabo rotaciones de funciones de onda Ψ en lugar de cuerpos rígidos). Por lo tanto, resulta deseable expresar las rotaciones del cuerpo rígido en términos de rotaciones de ejes fijos en el espacio. Para ello, podemos recurrir a la siguiente relación sencilla:
Esta expresión tiene la siguiente interpretación sencilla leída de derecha a izquierda: en primer lugar, giramos el eje-y’ del cuerpo rígido de regreso a la dirección del eje-y fijo en el espacio (como se ve desde el lado positivo del eje-z) dando un giro en torno al eje-z en un ángulo α. Tras la (segunda) rotación en un ángulo β, y finalmente, regresamos el eje-y a la dirección del eje-y’ (con una rotación en torno al eje-z fijo en el espacio, ¡no el eje-z’!) en un ángulo α. La expresión nos dice que el efecto neto combinado de las rotaciones es equivalente a una rotación sencilla en torno al eje-y’ en un ángulo β. Esto puede entenderse mejor tomando en las manos una armazón con tres varillas perpendiculares la una a la otra (representativas de los ejes fijos al cuerpo rígido) y dando los giros indicados. También se puede visualizar viendo el efecto de las rotaciones en el disco de la figura dada arriba para las rotaciones de Euler, en donde se puede comprobar que la orientación del eje-y’ del cuerpo rígido permanece inalterada como resultado de las operaciones. Más aún, la orientación del eje-z final del cuerpo rígido permanece igual ya sea que se aplique Ry'(β) o que se aplique la secuencia de operaciones Rz(α) Ry(β)Rz-1(α). En ambos casos, el eje-z del cuerpo rígido hace un ángulo polar β con el eje-z fijo en el espacio (el mismo que el eje-z inicial) y su ángulo azimutal α medido en el sistema de coordenadas fijas en el espacio.
De modo semejante, se puede comprobar la siguiente relación:
Combinando estas dos relaciones con lo anterior, se obtiene de manera directa:
Obsérvese que en los últimos pasos se ha utilizado el hecho de que las rotaciones sucesivas llevadas a cabo en torno a un mismo eje conmutan, esto es, Rz(γ) y Rz(α) conmutan.
En cuanto al orden de las rotaciones que queremos llevar a cabo, al efectuar tres rotaciones sucesivas (α,β,γ) sobre ejes distintos, estamos en plena libertad de escoger los ejes así como el orden de los ejes sobre los cuales se se llevarán a cabo las rotaciones. Podemos empezar con una rotación en torno al eje-x, seguida de una rotación en torno al eje-z, seguida de otra rotación en torno al eje-y, por ejemplo. O podemos empezar con una rotación en torno al eje-y, seguida de una rotación en torno al eje-x, seguida de otra rotación en torno al eje-z. Si se van a llevar a cabo tres rotaciones sucesivas, habiendo varias posibilidades de hacerlo, ¿qué combinación de rotaciones será la que más nos convenga para los análisis mecánico-cuánticos que se estarán llevando a cabo? Ya se señaló previamente en la entrada anterior que no es indispensable recurrir a los tres ejes coordenados Cartesianos, ya que con solo dos ejes que se utilicen resulta suficiente para especificar cualquier relocalización en el espacio tridimensional angular. Se acostumbra utilizar el eje-z para la primera rotación (rotación inicial) y la tercera rotación (rotación final), lo cual nos deja con la opción de utilizar ya sea el eje-x o el eje-y para la rotación final. ¿Cuál de los dos ejes nos conviene más? La respuesta nos llega observando que, en los operadores de rotación mecánico-cuánticos, la rotación intermedia es la que mezcla los distintos valores del número cuántico magnético m. Y en el caso de sistemas cuyo spin es 1/2, la selección obvia es la rotación que se lleva a cabo en torno al eje-y, para lo cual se utiliza como generador de la rotación a la matriz de Pauli σ2 (σy) que es precisamente la matriz cuyos elementos son todos imaginarios:
¿Y por qué habría de resultar más ventajoso usar una matriz cuyos elementos son imaginarios en vez de usar cualquiera de las otras dos matrices de Pauli cuyos elementos son números reales? ¿No es ésto un contrasentido? En realidad, no, porque al ver la definición del operador de rotación:
caemos en la cuenta de inmediato de que el número imaginario i que aparece dentro del exponente, al multiplicar las entradas imaginarias de la matriz σ2, produce una matriz cuyos elementos son todos números reales. Esto no se lograría si en lugar de usar una rotación en torno al eje-y se usara una rotación en torno al eje-x. Teniendo ya suficientes problemas para darle interpretación física a los resultados que se están obteniendo, resulta insensato usar alternativas que nos produzcan como resultado números imaginarios o complejos cuyo significado físico es menos intuitivo.
A continuación, y correspondiendo a rotaciones llevadas a cabo sobre funciones de onda que representan a partículas cuyo momento angular de spin es 1/2, siendo las matrices generadoras de la rotación las matrices de Pauli, los operadores de rotación en torno a cada eje, en base a lo que se ha visto en las entradas previas, son:
Supóngase que se tiene la siguiente secuencia de rotaciones de Euler en el orden indicado:
1) Una rotación en torno al eje-z en un ángulo γ.
2) Una rotación en torno al eje-y en un ángulo β.
3) Una rotación en torno al eje-z en un ángulo α.
El resultado combinado de estas rotaciones viene siendo:
que usando los operadores de rotación exponenciales para cada rotación específica resulta en lo siguiente:
En virtud de las propiedades de grupo de las rotaciones, esperamos que la secuencia arriba indicada de operaciones de rotación sea equivalente a una sola rotación sencilla en un ángulo θ con respecto a cierto eje. ¿Cómo se puede encontrar tal ángulo? Esto requiere repasar una propiedad importante de las matrices basada en la definición de la traza (o trazo) de una matriz como la suma de los elementos puestos a lo largo de la diagonal principal:
La traza de una matriz tiene varias propiedades peculiares que se pueden explotar ventajosamente en la simplificación de problemas por el simple hecho de que el proceso de diagonalización de una matriz conduce directamente a la definición de una traza. Haciendo un repaso rápido, para una matriz cuadrada 2×2:
se puede construír una matriz T que sea capaz de transformar a la matriz A en una matriz diagonal de la siguiente manera:
de modo tal que los autovalores propios característicos eigen de la matriz A, en este caso λ1 y λ2, aparezcan puestos en la diagonal principal. Tras la diagonalización, surge de modo natural el concepto de la traza:
Este concepto tiene propiedades importantes que serán demostradas a continuación.
PROBLEMA: (1) Dadas dos matrices cuadradas A y B, demuéstrese que:
(2) Demostrado lo anterior, demuéstrese que dos matrices que son equivalentes (por relaciones de similitud) tienen la misma traza, o sea que la traza es una propiedad matricial que se conserva al llevar a cabo operaciones de similitud.
(1) Simbólicamente, recurriendo a la sumatoria, la traza de una matriz A definida como la suma de los elementos que van puestos a lo largo de la diagonal principal, se escribe de la siguiente manera:
Considérese otra matriz B del mismo tamaño que la matriz A, cuya traza será:
Llámese C al producto de las dos matrices A y B en ese orden:
La definición matemática formal de cada elemento cij de la matriz C obtenido mediante la multiplicación de las dos matrices A y B en ese orden está dada por la relación:
Esta relación nos define la manera de obtener todos los elementos para la matriz C. Pero estamos interesados únicamente en los elementos diagonales de dicha matriz, para los cuales los sub-índices p y q son iguales:
Entonces, usando la definición de la traza sobre el producto A·B y desarrollando, se tiene:
(2) Usando el resultado que se acaba de obtener, se puede demostrar fácilmente que la traza de una matriz A sobre la cual se ha llevado a cabo una operación de similitud U†·A·U permanece invariante:
Ahora bien, tomando como punto de partida la rotación para un sistema físico de spin 1/2 basada en los ángulos de Euler:
se tiene además también que esta rotación es equivalente a la siguiente rotación llevada a cabo en torno a cierto eje n en un ángulo θ:
Puesto que ambas matrices son equivalentes, las trazas de las matrices deben ser iguales. En el caso de la primera matriz, sumando los elementos diagonales de dicha matriz se encuentra que la traza es:
mientras que en el caso de la segunda matriz al sumar sus elementos diagonales se encuentra que su traza es:
Siendo las trazas de ambas matrices iguales, se tiene entonces:
Esto demuestra que una secuencia de operaciones de rotación usando como parámetros a los ángulos de Euler es equivalente a una sola rotación sencilla en un ángulo θ con respecto a cierto eje.
A partir de este punto, y para estar en mayor conformidad con la notación empleada en una mayoría de los textos actuales, se hará un cambio notacional utilizando j como el símbolo de un momento angular de carácter general en lugar del símbolo l utilizado para denotar el momento angular orbital. Además, en lugar de la notación usual para las armónicas esféricas como funciones de onda se recurrirá a la representación de las mismas como kets. De este modo, los cambios notacionales son los siguientes:
De las entradas tituladas “Momento angular orbital: análisis ondulatorio”, tomaremos a continuación las relaciones de operadores escalera para el momento angular, que para el caso del operador escalera de subida o ascenso (en la escalera) es:
mientras que para el caso del operador escalera de bajada o descenso es:
Hemos visto ya que para extraer un elemento de una matriz Q situado en cierto renglón y en cierta columna de la matriz la operación indicada (véase la entrada “La notación bra-ket de Dirac”) es:
Del mismo modo, si se tiene un operador de carácter general como Jz, la operación requerida para extraer un elemento matricial de dicho operador será:
Obsérvese con cuidado que esto especifica la extracción de un elemento {m’,m} ubicado en una sub-matriz, la cual a su vez forma parte de un conjunto de sub-matrices {.j’,.j} que son a su vez elementos de una gran matriz, la matriz Jz (vease la entrada “Matrices y sub-matrices”). Puesto que en los operadores escalera que se tienen arriba, la acción de los mismos es sobre el número cuántico magnético m (que es el que sube y baja) manteniendo al número cuántico j constante, en este tipo de análisis resulta conveniente anclar a .j considerándolo igual tanto en el bra como en el ket:
Estando de acuerdo en lo anterior, podemos tratar de llevar a cabo la extracción de un elemento de un operador de rotación en notación bra-ket de la manera siguiente:
En realidad, lo que estamos haciendo aquí es definir al operador de rotación que ya se había visto previamente pero ahora usando la extracción de sus elementos matriciales en notación bra-ket:
Habiendo visto ya que para el operador de rotación expresado en su forma más general dicho operador tiene una representación exponencial, se puede escribir entonces:
Habiendo obtenido la matriz general de rotación en función de ángulos de Euler para sistemas físicos cuyo momento angular es 1/2, el siguiente paso lógico consiste en obtener la matriz general de rotación para sistemas físicos cuyo momento angular es j.=.1. De antemano damos por hecho de que se tendrá que recurrir a matrices de orden 3×3. Al igual que en el caso j.=.1/2, resultará conveniente especificar un operador de rotación de carácter general de modo tal que la primera rotación se lleve a cabo en torno al eje-z, la segunda rotación se llevará a cabo en torno al eje-y, y la tercera rotación se llevará a cabo en torno al eje-z. De este modo, lo que se busca es la manera de especificar los elementos de la matriz que resulta de la operación combinada:
Recurriendo a los operadores exponenciales usados para evaluar cada una de estas rotaciones, se tiene:
Se puede llevar a cabo una simplificación en lo que concierne a las rotaciones en torno al eje-z, recurriendo a la siguiente relación del momento angular que ya se había estudiado previamente al llevarse a cabo las primeras introducciones al momento angular orbital:
Apoyándonos en esta relación, podemos justificar el siguiente procedimiento:
Puesto que obtenemos algo similar en lo que concierne a la rotación llevada a cabo en torno al eje-z en una magnitud angular α, siendo los ángulos α y γ cantidades numéricas constantes al igual que los números cuánticos magnéticos m y m’, esto implica que podemos sacar fuera un factor exponencial teniendo entonces:
Este resultado intermedio nos confirma que es la segunda rotación, la que se lleva a cabo en torno al eje-y, la única rotación que no es trivial por ser la que mezcla los distintos valores del número cuántico magnético m. Esto nos deja ahora con el problema de tener que evaluar:
se tiene que obtener primero la matriz Jy. Para ello, utilizaremos los operadores escalera del momento angular dados arriba, y la relación:
Por lo que ya se vió previamente al introducirse el tema del momento angular orbital desde la perspectiva de la Mecánica Ondulatoria, una evaluación típica de los elementos matriciales de los operadores escalera (para la combinación de valores j.=.1, m.=.0 y m’.=.1) arroja los siguientes resultados:
De este modo, se obtiene el siguiente valor de Jy para j.=.1, m.=.0 y m’.=.1:
Procediendo de igual manera, se obtienen todos los demás elementos restantes con los cuales se puede construír la matriz Jy:
Teniendo la matriz Jy, se puede proceder a evaluar el exponencial que representa al operador de rotación correspondiente. Para ello, obsérvese que:
y así sucesivamente. Esto se puede generalizar para cualquier exponente dependiendo de que el exponente sea par o impar:
Con estas relaciones (las cuales desafortunadamente son válidas únicamente para el caso j.=.1 y no se pueden ampliar a otros valores del momento angular) podemos evaluar directamente el exponencial mediante un desarrollo de Taylor en series de potencias, sumando por separado los términos para los cuales los exponentes son pares y los términos para los cuales los exponentes son impares:
El término más fácil de evaluar es el que está elevado a la potencia cero, quitándole un término a la primera sumatoria:
Esto se puede seguir simplificando usando las series de potencias conocidas para las funciones trigonométricas, con lo cual lo anterior nos viene quedando como:
Insertando en esto último la matriz Jy obtenida arriba y sumando los componentes matriciales respectivos, se obtiene la siguiente matriz reducida de rotación:
El procedimiento que se ha empleado aquí para obtener en su forma matricial explícita este último operador de rotación obviamente se vuelve laborioso para valores del momento angular mayores a j.=.1, y resulta sumamente deseable buscar atajos que permitan llevar a cabo esta labor de una manera más metódica y simplificada. Afortunadamente, tal atajo existe.
Casi al final de la entrada “Los grupos de rotación II” se puso como ejemplo de un operador de rotación especificado en ángulos de Euler aquél para el cual el número cuántico es l.=.1, señalándose que los elementos de un operador de rotación como ése pueden ser obtenidos con la ayuda de una fórmula conocida como la fórmula de Wigner, la cual veremos ahora en mayor detalle. La fórmula es la siguiente:
Al usar esta fórmula, la sumatoria se lleva a cabo siempre y cuando ninguno de los argumentos factoriales en el denominador sea negativo.
A continuación, se evaluarán tres de los elementos matriciales generados por la fórmula de Wigner para el mismo operador de rotación que fue puesto como ejemplo al final de la entrada “Los grupos de rotación II”. El primer elemento matricial que será evaluado es el siguiente llevando a cabo la substitución numérica directa de los valores de l, m y m’ indicados:
l.=.1, m.=.1, m’.=.1:
Simplificando:
Debido a la presencia de factoriales negativos en el denominador que corresponde al primer factor de la sumatoria, todos los sumandos posibles se desvanecen exceptuando el término para el cual k.=.0. Por lo tanto, poniendo k.=.0:
Usando la identidad trigonométrica:
se tiene entonces:
Este es el primer elemento matricial que encabezó la lista de elementos matriciales puestos casi al final de la entrada “Operadores de rotación II”.
A continuación se evaluará un segundo elemento usando los valores:
l.=.1, m.=.-1, m’.=.-1:
En este caso, la sumación corre desde k.=.0 hasta:
k.=.j + m.=.1 - 1.=.0
habiendo por lo tanto un solo término para ser calculado en la sumación, el que corresponde a k.=.0:
Simplificando:
A continuación se evaluará un tercer elemento usando los valores:
l.=.1, m.=.0, m’.=.0:
Simplificando:
En este caso, no hay factoriales negativos, y la sumatoria nos requiere la suma de dos términos:
Por lo tanto:
Obsérvese cómo se van obteniendo uno a uno los elementos de la misma matriz de rotación que se construyó arriba sin el beneficio de la fórmula de Wigner. Obsérvese además cómo la fórmula de Wigner produce el operador de rotación completo incorporando (como factores de fase) los efectos de las rotaciones inicial y final en torno al eje-z. Procediendo del mismo modo, se pueden evaluar todos los nueve elementos matriciales del operador de rotación para. j.=.1.
En lugar de trabajar en forma rigurosa y axiomática derivando primero la fórmula de Wigner para después ilustrarla con ejemplos como los que se han presentado arriba, por razones pedagógicas y didácticas se ha optado por mostrar primero la forma en la cual se utiliza dicha fórmula, lo cual hará más claro no sólo su procedimiento de derivación sino que dará un aliciente para indagar la manera en la cual se obtiene dicha fórmula, lo cual se verá en mayor detalle en la siguiente entrada.