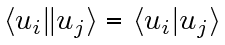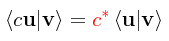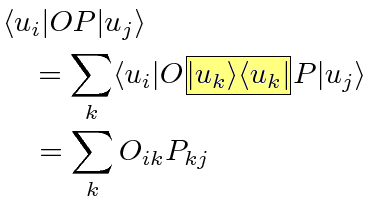Considérese la siguiente representación del vector x = (x1, x2, x3) que podemos llevar a cabo utilizando vectores unitarios de base (los super-índices no son exponentes):
x = x1(1, 0, 0) + x2(0, 1, 0) + (0, 0, x3)
Ahora supóngase que llevamos a cabo la misma representación usando vectores columna en lugar de vectores renglón, identificando tras esto a cada vector columna de una manera que al principio parecerá algo peculiar:
La representación que tenemos destacada de color amarillo formada por una línea vertical a la izquierda y un paréntesis angulado a la derecha es esencialmente lo que llamamos un ket.
Retendremos la convención según la cual dada una cantidad compleja z cualesquiera:
z = x + iy
el conjugado complejo de dicha cantidad se representa con un asterisco puesto como super-índice:
z* = x - iy
La notación bra-ket de Dirac se basa en dos símbolos fundamentales, siendo uno de ellos el bra:
y siendo el otro el ket:
El uso más sencillo de ambos símbolos consiste en unirlos para representar con ello el producto interno de dos vectores o dos funciones. Cuando esto se hace, el bra siempre se pone a la izquierda, y el ket siempre se pone a la derecha, estando de este modo encerrado todo entre dos paréntesis angulados (las palabras bra y ket derivan de la palabra inglesa bracket).
La operación más sencilla que se puede llevar a cabo consiste en la adición de dos kets:
Para que dos kets puedan ser sumados, deben ser del mismo tipo, lo cual implica que no podemos sumar las funciones de onda propias de la Mecánica Ondulatoria a los vectores y matrices propios de la Mecánica Matricial, y si vamos a sumar vectores y matrices propios de la Mecánica Matricial éstos tienen que ser del mismo tipo. A modo de ejemplo, si partimos de las siguientes dos funciones de onda:
entonces tras representar estas funciones de onda como kets:
podemos representar la adición de dichos kets en la notación de Dirac de la manera siguiente:
PROBLEMA: Sumar todos los kets que sea posible sumar de los mostrados a continuación:
Puesto que para poder sumar dos kets estos tienen que ser del mismo tipo, las únicas sumas de kets que pueden ser llevadas a cabo aquí son las siguientes:
Cada ket puede ser multiplicado por una constante numérica cuyo cuadrado dá la probabilidad de ocurrencia del estado representado por el ket, de modo tal que podemos hacer combinaciones como la siguiente:
en la cual la probabilidad de que en un experimento se dé el estado simbolizado por el primer ket es |a|² y la probabilidad de que se dé el estado simbolizado por el segundo ket es |b|² . Por lo general, cuando se suman dos o más kets lo que tenemos es una superposición de estados que dá lugar a una nueva situación, como lo muestra la siguiente figura en la cual tenemos una suma de dos los únicos dos estados posibles:
Habiendo únicamente dos estados posibles en el ejemplo que se acaba de dar, la relación de abajo nos indica que la suma de las probabilidades de obtener cualquiera de los dos estados debe ser igual a la unidad, a la certeza.
Tanto en el Analisis Vectorial como en el Algebra Lineal estamos familiarizados con el concepto del producto escalar o producto interno de dos vectores a y b definido en su quintaesencia en un espacio tridimensional Euclideano como el producto de las magnitudes de dichos vectores multiplicado por el coseno del ángulo que forman dichos vectores.
a · b = |a| |b| cos(θ)
Bajo un sistema de coordendas rectangulares Cartesianas en donde cada uno de los vectores a y b esté especificado por las tres componentes que son iguales a sus proyecciones sobre cada uno de los ejes coordenados:
a = (a1 , a2 , a3)
b = (b1 , b2 , b3)
en donde las componentes vectoriales son números reales, no resulta difícil el comprobar que el producto interno de los vectores a y b en función de sus componentes sobre los ejes coordenados está dado por la siguiente relación:
a · b = a1b1 + a2b2 + a3b3
Si queremos definir un concepto similar dentro de la Mecánica Cuántica, el problema que se nos presenta de inmediato es que las componentes de los vectores no sólo pueden ser números reales, también pueden ser números complejos o imaginarios. Necesitamos antes que nada redefinir de alguna manera, desde el punto de vista estrictamente matemático sin entrar todavía a ningún detalle, el concepto de producto interno de dos cantidades cuando una de ellas o ambas pueden ser números complejos. Se ha comprobado en la práctica que una de las formas más convenientes de hacerlo es de la manera siguiente:
en donde el asterisco para los componentes del vector a (destacados de color rojo) indica que se debe tomar el conjugado complejo del elemento (invirtiendo el signo del factor imaginario i en donde lo haya). Obsérvese que aquí se ha dado un paso importante, se ha supuesto que la definición será válida para vectores con una dimensión mayor que tres, lo cual aunque no tenga mucho sentida desde el punto de vista físico sí puede ser adoptado desde el punto de vista matemático sin problema alguno. Obsérvese también que el orden en el cual se especifica el producto de los vectores a y b es importante, ya que si se sigue un orden inverso entonces de acuerdo a la definición que se acaba de dar el producto interno será:
Resalta el hecho de que, bajo esta definición, el producto interno de dos vectores no es conmutativo. Sin embargo, observando el hecho de que si tomamos el conjugado complejo en ambos miembros de la igualdad anterior (usando el hecho de que el conjugado de la suma de números complejos es igual a la suma de sus conjugados complejos, y el hecho de que el conjugado complejo de un producto es igual al producto de los conjugados):
Esto significa que:
En la Mecánica Matricial, representamos el producto interno de dos vectores xi y xj con la notación bra-ket simbolizado de la siguiente manera con un bra puesto a la izquierda unido a un ket puesto a la derecha juntando ambos bra y ket de la siguiente manera:
Obsérvese que al llevarse a cabo la unión de un bra con un ket la doble línea vertical que se forma con la línea vertical venida del bra y la línea vertical venida del ket se “funden” en una sola línea vertical (“|”). Esto es algo que siempre se hace cuando surgen dobles líneas verticales en operaciones llevadas a cabo con bras y kets. Siendo el producto interno de dos vectores un número, lo que tenemos arriba es esencialmente un número.
Tomando como base la conclusión que se había obtenido para dos vectores con componentes complejos:
procediendo por analogía podemos asentar como relación fundamental para la definición del producto interno entre un bra y un ket lo siguiente:
El caso más frecuente en la Mecánica Cuántica es que los componentes que son usados a modo de vectores que sean ortogonales (independientes el uno del otro) estando cada uno de ellos normalizado (con su longitud igual a la unidad), o sea, vectores ortonormales. En este caso, podemos destacar el uso de vectores normalizados con algún otro tipo de notación, por ejemplo ui y uj, juntando ambos bra y ket de igual manera:
En este caso, cuando los vectores ui y uj son vectores ortogonales y normalizados, esto es, ortonormales, entonces el producto interno de los mismos debe ser el siguiente:
En esta definición utilizamos el delta de Kronecker para el cual δij.=.1 cuando i.=.j y δij.=.0 cuando i.≠.j. El bra asignado al vector ui le dá una representación matricial como un vector renglón, mientras que el ket asignado al vector uj le dá una representación matricial como un vector columna. Si se trata del mismo vector, con i.=.j, entonces la longitud del vector es 1 puesto que el vector se supone que está normalizado, y si se trata de dos vectores diferentes tomados de la misma base entonces con i.≠.j el producto interno es igual a cero reflejando el hecho de que los dos vectores son ortogonales.
A todo ket le podemos asignar un bra que es su dual correspondiente. Dado un ket, podemos obtener su bra dual tomando el conjugado complejo del ket, lo cual significa cambiarle el signo a todas las instancias en donde aparezca el número imaginario i.
PROBLEMA: Dado el siguiente ket:
obténgase un bra que sea su dual de modo tal que al tomar el producto interno de ambos el resultado sea igual a la unidad.
Puesto que la longitud del ket proporcionado no es igual a la unidad, multiplicaremos dicho ket por una constante de normalización A:
El bra que corresponde a este ket lo obtenemos tomando el conjugado complejo del ket:
Para que el producto de este bra con su ket que es su dual sea igual a la unidad, la condición de normalización requiere que:
Con esta condición podemos obtener la constante de normalización A:
De este modo, tanto el bra como el ket normalizados que forman un par dual son los siguientes:
En forma similar a como lo hacemos con los vectores de la Mecánica Matricial, en la Mecánica Ondulatoria representamos el producto interno de dos funciones del mismo tipo pero con un número cuántico diferente de una manera como la siguiente:
En general, dadas dos funciones ψ y φ, la notación bra-ket:
representa algo como:
Aunque tengamos dos funciones diferentes ψ(x) y φ(x), estas deben estar definidas sobre el mismo espacio vectorial (de la misma dimensión), y para llevarse a cabo el producto interno de las mismas tomamos el conjugado complejo de la función que aparece en el bra, en este caso ψ*(x), para que el resultado final sea un número real, ya que si el resultado final fuese un número imaginario o complejo la base matemática no nos sirve para representar cantidades físicas en la Mecánica Cuántica.
PROBLEMA: Demostrar que:
La demostración pedida se puede llevar a cabo de la siguiente manera:
En general, podemos sacar constantes fuera de un producto bra-ket, siempre y cuando se tenga cuidado de observar en qué parte del producto bra-ket se encuentra la constante que será sacada fuera, ya sea en el bra o en el ket. Si una constante K se encuentra en el bra, entonces al ser sacada fuera debe salir como el conjugado complejo de K, esto es, como K*; y si la constante se encuentra en el ket, entonces al ser sacada fuera deberá salir tal cual, esto es, como K, sin que se le tome su conjugado complejo al sacarla fuera.
En términos de algo que los matemáticos puros reconocen como un espacio funcional (el cual es tema de estudio del Análisis Funcional que a su vez trata acerca de las funciones de funciones), podemos concebir al bra como una instrucción para llevar a cabo la siguiente operación:
sobre algo que se le ponga al bra del lado derecho, en donde el “hueco” simbolizado como AA representa el espacio vacío a espera de ser llenado por la función que el bra encuente a su lado derecho, por ejemplo el ket que representa a la función m:
PROBLEMA: Demostrar, usando la notación bra-ket para ello, que el siguiente conjunto de funciones:
es un conjunto ortonormal. ¿Cuál será la dimensión del espacio vectorial en este problema?
Evaluaremos primero el producto interno de la función ψ0 consigo misma:
Puesto que el producto interno de la función ψ0 consigo misma es igual a la unidad, podemos ver que la función está normalizada.
Ahora evaluaremos el producto interno de la función ψ1 consigo misma:
Puesto que el producto interno de la función ψ1 consigo misma también es igual a la unidad, podemos ver que la función también está normalizada.
En general, para cualquiera de las funciones ψn del conjunto, tenemos:
Resulta claro que todas las funciones están normalizadas.
Falta ver si las funciones son ortogonales entre sí, para lo cual tenemos que evaluar el siguiente producto interno:
siendo m ≠ n. Recurriendo a la fórmula de Euler:
tenemos entonces dos integrales a evaluar:
Llevando a cabo ambas integraciones:
El segundo término (destacado en color rojo), siendo una función par, al ser evaluado entre los límites -1 y +1 se vuelve cero, dejándonos únicamente con el primer término, que tras la toma de límites se vuelve:
Por hipótesis, estamos considerando que m y n son dos enteros diferentes. En tal caso, el argumento de la función senoidal será un múltiplo entero de π. Pero el seno de un múltiplo entero de π siempre será igual a cero. Entonces, cuando m y n son diferentes, el producto interno las dos funciones de onda será igual a cero, esto es, serán ortogonales.
Se concluye que el conjunto dado de funciones es ortonormal, esto es, ortogonales entre sí y normalizadas a la unidad, lo cual podemos expresar con la ayuda del delta de Kronecker:
cumpliéndose de este modo la condición para que un conjunto de funciones pueda ser considerado una base ortonormal.
Puesto que tenemos un total de 9 funciones independientes la una de la otra, la dimensión del espacio vectorial en este problema es igual a 9. Si utilizamos un número adicional de funciones similares, puesto que para un sub-índice máximo N tenemos 2N+1 vectores (funciones) de base linealmente independientes la dimensión del espacio vectorial será igual a 2N+1.
Si tenemos una función ψ expandible sobre una representación en series ortogonales como es el caso de las series de Fourier en las que la función periódica que está siendo expandida es igual a la suma de una cantidad infinitamente grande de las amplitudes de una frecuencia fundamental y sus harmónicas, podemos entresacar una de las componentes de la serie (ψi) en particular tomando el producto interno de la siguiente manera:
La expansión de una función ψ en una serie infinita de componentes ψi separados el uno del otro con los componentes ui tomados de una base ortonormal se representa de la siguiente manera:
En la notación bra-ket tenemos además operadores. Por regla general, un operador O actúa sobre un ket que está puesto a su derecha. En la Mecánica Matricial, el operador por lo general es una matriz que actúa sobre un vector u:
mientras que en la Mecánica Ondulatoria el operador puede ser un operador diferencial actuando sobre una función de onda ψ:
Un operador, después de haber actuado sobre un ket, generalmente resulta en otro ket, el cual puede ser utilizado para formar posteriormente un producto con un bra:
En la Mecánica Ondulatoria hemos visto ya que una cantidad observable tal como la energía que pueda ser representada como un operador actúa sobre una función de onda en una eigen-ecuación que nos regresa (del lado derecho de la eigen-ecuación) la función de onda multiplicada por una cantidad λ que es a su vez el eigenvalor que se medirá en el laboratorio relacionado con dicha observable:
siendo ψ la eigenfunción de onda asociada con el eigenvalor. Con la notación bra-ket, la representación de algo como lo anterior se lleva a cabo utilizando kets sobre los cuales actúa el operador que los antecede:
escribiéndose entonces una eigen-ecuación del modo siguiente:
En un sistema con estados ligados, habrá ciertos kets de importancia especial, los eigenkets propios del sistema, que podemos denotar como:
con la propiedad de que:
en donde a, b, c, ... son simples números (las cantidades observables a ser medidas con algún aparato). El conjunto de números:
es el conjunto de eigenvalores del operador.
Habiendo visto que existe una dualidad importante entre los bras y los kets, esto nos sugiere que un operador no sólo debe ser capaz de actuar sobre kets, también debe ser capaz de actuar sobre bras, lo cual resulta ser cierto aquí, excepto que para que un operador pueda actuar sobre un bra tiene que hacerlo sobre el bra que está situado inmediatamente a su izquierda.
Un operador X actúa siempre sobre el ket que está situado a su derecha, y el producto resultante viene siendo otro ket:
Un operador X actúa siempre sobre el bra que está situado a su izquierda, y el producto resultante viene siendo otro bra:
Adaptarse a esta nueva realidad requiere algo de práctica, del mismo modo que una persona que toda su vida ha estado acostumbrada a escribir con su mano derecha no necesariamente empezará a escribir de inmediato con su mano izquierda con la misma facilidad. La eigen-ecuación en la cual se utiliza un bra en lugar de un ket es la siguiente:
Este detalle nos permite llevar a cabo de una manera sencilla algunas demostraciones que de otra manera nos confundirían fácilmente al obscurecerse los detalles con la notación.
Si el operador O es una matriz, y si lo que queremos hacer es entresacar cierto componente de la matriz, lo hacemos tomando el triple producto matricial que se muestra a continuación:
En esta representación, se utiliza el bra para simbolizar un vector renglón ui, y el ket para simbolizar un vector columna uj. El producto matricial de O con uj nos entresaca una columna completa de la matriz O, la columna j, mientras que el producto posterior de ui con O nos entresaca el elemento situado en el renglón i del vector columna obtenido de la operación previa, dándonos de este modo el elemento Oij de la matriz O.
PROBLEMA: Definir el bra y el ket requeridos para entresacar de la siguiente matriz:
el elemento situado en el segundo renglón y en la tercera columna.
El elemento situado en el segundo renglón y en la tercera columna es el número 2. Lo podemos extraer de la siguiente manera con el producto matricial triple mostrado:
La multiplicación de la segunda matriz por la tercera matriz nos producirá un vector columna cuyos elementos serán todos los elementos de la tercera columna de la segunda matriz, entre los cuales está el número 2 que queremos entresacar. Y la multiplicación de la primera matriz por la matriz resultante de la operación anterior nos producirá una matriz de un solo elemento, que es el número 2. Entonces el bra y el ket requeridos para la extracción vienen siendo los siguientes:
En las expresiones que se muestran a continuación:
tenemos un operador matricial X al cual con la expresión en la primera línea se le entresaca el elemento situado en el primer renglón y la primera columna de la matriz, en la segunda línea se tiene al elemento situado en el segundo renglón y en la segunda columna de la matriz, en la tercera línea se tiene al elemento situado en el tercer renglón y en la tercera columna de la matriz, y así sucesivamente. Puesto que, por definición, la suma de los elementos de una matriz situados a lo largo de su diagonal principal se define como la traza de la matriz, esto nos permite definir la traza de un operador de la siguiente manera:
En notación bra-ket, representamos una expansión Fourier (sobre cualquier base de funciones ortonormales, no necesariamente trigonométricas) de la siguiente manera:
PROBLEMA: Ya se ha visto previamente que cuando el conmutador de Born de dos operadores es igual a cero, se tienen observables compatibles que pueden ser medidas simultáneamente sin límite teórico a la precisión de las mediciones simultáneas que se llevan a cabo. Supóngase que se tienen dos observables compatibles cuyos operadores asociados son A y B, y supóngase que los eigenvalores de A no son degenerados formando los mismos una matriz diagonal. Demuéstrese entonces que los elementos matriciales del operador B también serán todos diagonales (esto es, la matriz asociada con el operador B será también una matriz diagonal).
La condición de Born para dos observables compatibles es la siguiente:
“Encapsulando” ambos lados de lo anterior entre un bra y un ket, tenemos entonces el siguiente desarrollo:
Obsérvese que en la sexta línea del desarrollo, mientras que en el segundo término se ha hecho actuar al operador A sobre el ket que está a su derecha devolviéndonos el ket y el eigenvalor a (un número) con el cual está asociado el ket, en el primer término se ha hecho actuar al operador A sobre el bra que está a la izquierda devolviéndonos un ket y el eigenvalor b con el cual está asociado el ket. De la séptima línea podemos ver que para a.≠.b la única manera en la cual la expresión obtenida puede ser cierta será teniendo:
lo cual es la principal característica de una matriz diagonal. Y para a.=.b, la expresión será válida aunque ninguno de los elementos del operador B sea igual a cero. Entonces la matriz B es una matriz diagonal. Esto refleja algo que habíamos visto con anterioridad: para que dos matrices sean conmutativas (generalmente hablando, dejando fuera los casos triviales) ambas matrices deben ser diagonales, o deben poder ser diagonalizadas simultáneamente.
Ahora bien, al actuar un operador O sobre un ket que representa a una función que puede ser expandida en una serie ya sea finita o infinita de funciones ortonormales de base, en la notación bra-ket esto permite meter el operador O dentro de la sumatoria para actuar directamente sobre las funciones de base usadas para la expansión de una función ψ:
Podemos hacer operaciones con bras y kets haciendo substituciones como sea necesario a nuestros propósitos, tal como aplicar un bra a la anterior expansión Fourier para obtener lo siguiente:
Supóngase ahora que tenemos un conjunto ortonormal completo de funciones ψj que satisface que satisface la definición de ortonormalidad:
Puesto que los ψj forman un conjunto completo, cualquier función de onda ψ permisible puede ser expandida (expansión de Fourier) sobre dicho conjunto de funciones ortonormales:
Del mismo modo:
Supóngase ahora un operador Q que actúa sobre una función de onda tal:
Multiplicando ambos miembros por el conjugado complejo ψk* de ψk e integrando sobre todo el espacio:

En la expresión que tenemos del lado derecho de la igualdad, podemos sacar fuera de la integral el símbolo de la sumación, ya que generalmente hablando los signos de integración y sumación son intercambiables, además de sacar fuera también a las constantes a'j:
Pero lo que tenemos en el lado derecho de la igualdad ya había sido definido como algo que cumple con la condición de ortonormalidad por ser el conjunto de funciones ψj que satisface la definición de ortonormalidad, o sea:
Obsérvese que en el paso intermedio se ha aplicado la propiedad del delta de Kronecker que elimina todos los términos de la sumatoria excepto aquél término para el cual j.=.k. Entonces esto nos deja en nuestra relación inicial lo siguiente:
Podemos compactar esto mediante la notación bra-ket de Dirac teniendo entonces:
Obsérvese que en la segunda línea se ha substituído el producto bra-ket por Qkj, definido como un elemento matricial del operador Q:
En notación matricial lo que hemos obtenido lo podemos escribir de la siguiente manera:
Qa = a'
¿Hemos dejado de trabajar entonces con la Mecánica Ondulatoria y estamos trabajando ya plenamente dentro de la Mecánica Matricial? No precisamente, porque al hablar de un elemento matricial Qkj del operador Q estamos hablando de un operador Q que no necesariamente es una matriz convencional. El elemento Qkj del operador Q, en el desarrollo empleado para obtenerlo, depende no de otras matrices o vectores sino de funciones de onda que ciertamente no son matrices. De cualquier manera, la potencia de la notación bra-ket de Dirac es que los resultados que se obtengan mediante la misma puede hacerse extensible tanto a la Mecánica Matricial como a la Mecánica Ondulatoria sin cambio alguno, lo cual nos viene a confirmar nuevamente que pese al hecho innegable de que ambas ramas de la Mecánica Cuántica utilizan técnicas matemáticas diferentes en el fondo reflejan la misma filosofía estructural, ya que de no ser así entonces la Mecánica Matricial y la Mecánica Ondulatoria podrían predecir resultados diferentes para un mismo experimento, lo cual sería una verdadera calamidad para quienes creen en la unificación teórica de la Física.
Puesto que los bras y los kets no son operadores, se sobreentiende que si dos kets están escritos en sucesión uno tras otro dentro de una expresión, los kets pueden ser intercambiados de posición sin que esto resulte en consecuencias mayores, un hecho que puede ser utilizado ventajosamente en la simplificación de expresiones. Podemos llamar a este hecho la conmutatividad de los kets:
Del mismo modo, se sobreentiende también que si dos bras están escritos en sucesión uno tras otro dentro de una expresión, los bras pueden ser intercambiados de posición sin que esto resulte en consecuencias mayores, un hecho que puede ser utilizado ventajosamente en la simplificación de expresiones. Podemos llamar a este hecho la conmutatividad de los bras:
En rigor de verdad, dos kets en sucesión uno tras otro es una circunstancia que pudiéramos considerar ilegal, al igual que dos bras en sucesión uno tras otro. Sin embargo, esta es una situación que puede surgir (y de hecho surge) en algún paso intermedio de algún desarrollo que estemos llevando a cabo. Si el lector siente alguna incomodidad con lo que tenemos arriba, se pueden agregar paréntesis para volver ambas expresiones “legales”:
Ahora bien, si formamos un producto matricial con un bra puesto a la izquierda y con un ket puesto a la derecha, ya hemos visto que obtendremos un número como el resultado de ese producto interno. Pero si formamos un producto con un ket puesto a la izquierda y un bra puesto a la derecha, entonces el resultado de esa operación será indudablemente una matriz. Y si los vectores que son utilizados para formar dicha matriz son ortonormales, el resultado será indudablemente la matriz identidad I. Se acostumbra representar esto de la siguiente manera:
Si estamos pensando en los uk como vectores ortonormales, esto último tal vez pueda parecer un poco desconcertante, puesto que aparentemente tenemos en el lado izquierdo el número 1 en lugar de la matriz identidad I, mientras que en el lado izquierdo tenemos una sumación. Es en estos casos en los que, dentro de la Mecánica Matricial, se sobreentiende que el 1 en realidad representa a la matriz identidad (algo que desafortunadamente muchos textos no aclaran). Y la sumación en el lado izquierdo es el resultado lógico de la sumación de los vectores para formar una matriz. De cualquier modo, dentro de la Mecánica Ondulatoria, el 1 no representa la matriz identidad sino que es realmente el número 1.
PROBLEMA: Demostrar que:
Expandiendo la sumatoria, vemos que tenemos que evaluar lo siguiente:
Tomando para los vectores de base:
u1 = (1, 0, 0)
u2 = (0, 1, 0)
u3 = (0, 0, 1)
u2 = (0, 1, 0)
u3 = (0, 0, 1)
empezamos escribiendo u1 en notación ket como un vector columna y en notación bra como un vector renglón:
De este modo, al bra lo podemos tomar como una matriz 3x1 y al ket lo podemos tomar como una matriz 1x3, y de acuerdo con las reglas de multiplicación para las matrices el producto matricial en el orden ket-bra está definido en virtud de que el número de columnas que corresponde al ket (que es 1) es igual al número de renglones que corresponde al bra (que es también 1), siendo el resultado una matriz 3x3. De este modo, el producto de ambos en el orden ket-bra nos genera la siguiente matriz:
Escribimos ahora u2 en notación ket como un vector columna y en notación bra como un vector renglón:
En este caso, el producto de ambos en el orden ket-bra nos genera la siguiente matriz:
Por último, escribimos a u3 en notación ket como un vector columna y en notación bra como un vector renglón:
En este caso, el producto de ambos en el orden ket-bra nos genera la siguiente matriz:
Sólo nos queda ya llevar a cabo la suma de términos para poder obtener el resultado final:
Debe ser claro que este resultado será valido tanto para un espacio vectorial finito (como el de este problema que es de dimensión tres) como para un espacio vectorial infinito, siempre y cuando las funciones de base sigan siendo ortonormales.
PROBLEMA: Supóngase que el operador Hamiltoniano de energía de un sistema de dos estados está definido de la siguiente manera:
en donde ξ es una constante con unidades de energía. Encuéntrese para este sistema los eigenvalores de su energía así como las eigenfunciones que corresponden a estos valores expresadas como una combinación lineal de los kets |1> y |2>.
Empezaremos por simplificar un poco la expresión proporcionada para el Hamiltoniano:
Definiremos a continuación los ket de base de la siguiente manera:
Definidos así los kets de base, entonces los bras que son duales a estos kets lógicamente serán:
Lo que está entre los paréntesis en la expresión para el Hamiltoniano es simplemente la suma de cuatro productos externos, que evaluada como lo hemos visto con anterioridad nos proporciona la siguiente expresión:
La ecuación esencial, esto es, la ecuación de Schrödinger independiente del tiempo, fija la eigen-ecuación del Hamiltoniano de la siguiente manera:
Puesto que estamos considerando que se trata de un sistema de dos estados, podemos representar la función de onda como:
La eigen-ecuación matricial se puede escribir del modo siguiente:
Juntando en la eigen-ecuación lo que tenemos arriba, se llega entonces al siguiente determinante:
La solución del determinante nos conduce a los eigenvalores que son posibles para este sistema de dos estados:
Repitiendo mecánicamente los mismos pasos que fueron dados al principio de esta obra en las entradas “Vectores y matrices”, llegamos entonces a la siguiente solución para el eigenvalor con signo positivo:
Obsérvese cómo, para mantener consistencia en la notación, se ha representado a la función de onda (resaltada con color magenta) como un ket. Esta eigen-función de onda no está normalizada. Normalizándola de la manera usual, obtenemos:
En lo que respecta a la solución para el eigenvalor con signo negativo, se tiene:
que una vez normalizada viene siendo:
De este modo, las eigen-ecuaciones para este sistema de dos estados, en notación bra-ket, vienen siendo las siguientes:
Reflejando el hecho de que en el álgebra bra-ket trabajamos con operadores que pueden representar matrices, quizá la que puede ser considerada como la propiedad más importante de las operaciones matriciales, el axioma asociativo de multiplicación, aparece también al estar llevando a cabo operaciones “legales” de multiplicación dentro del álgebra bra-ket:
(A·B)·C = A·(B·C)
Esto significa que el siguiente producto, el cual representa a un operador actuando sobre un ket:
puede ser considerado igual a lo siguiente tras un reacomodo de los paréntesis de acuerdo al axioma asociativo de multiplicación:
ya que:
Con esto confirmamos que un operador actuando sobre un ket será igual a otro ket (sin tomar en cuenta la constante multiplicativa numérica que aparece como resultado de la operación). Esto significa que, si prescindimos de los paréntesis, podemos interpretar la siguiente expresión:
de dos maneras, ya sea como el operador |α><β| actuando sobre el ket |γ>, o equivalentemente como el número <β|γ> multiplicando al ket |α>. Aunque esto puede parecer ambiguo, en realidad la situación no es tan mala como parece, ya que este hecho sencillo permite llevar a cabo simplificaciones abreviadas.
Puesto que la multiplicación de un vector (o una matriz) por la matriz identidad nos regresa el mismo vector (o la misma matriz) sin alterar en nada lo que ya teníamos, lo anterior puede ser utilizado ventajosamente para injertarlo entre los símbolos de un producto interno bra-ket permitiéndonos un desarrollo posterior, como lo muestra el siguiente ejemplo en el que tenemos el producto de dos operadores O y P dentro de un producto interno bra-ket:
Obsérvese que cada vez que se injerta un producto bra-ket (en ese orden) usando funciones de base normalizadas, es necesario anteceder también una sumatoria por cada producto bra-ket injertado. Si hubiésemos injertado dos productos bra-ket usando funciones de base normalizadas, habríamos tenido que anteceder todo con dos sumatorias, y así sucesivamente. Lo que tenemos en amarillo es algo que hemos injertado dentro del producto interno original, y siendo la unidad no nos debe cambiar en nada la evaluación de lo que obtenemos posteriormente. Pero observando más de cerca, podemos ver que al haber hecho la operación que hemos hecho tenemos en esencia dos operaciones nuevas dentro de la sumatoria; una de ellas nos entresaca el elemento Oik del operador matricial O, mientras que la que le sigue nos entresaca el elemento Pkj del operador matricial P, tal y como lo hemos visto arriba.
Si con las operaciones definidas arriba entresacamos un elemento (O†) ij de la transconjugada de una matriz O, entonces esto puede representarse en la primera línea del siguiente desarrollo como se muestra a continuación:
Obsérvese que en la segunda línea del desarrollo hemos utilizado la propiedad de que matriz es en esencia una matriz Hermitiana, o mejor dicho, un operador Hermitiano. En la tercera línea, hemos invetido el orden de los bras y los kets, tomando al mismo tiempo el conjugado completo del elemento. Y en la cuarta línea, lo que tenemos es el conjugado complejo de la transpuesta de la matriz O, que es en esencia la definición de una matriz Hermitiana.
La notación bra-ket de Dirac además de ser elegante es sumamente versátil, permitiéndonos expresar en forma compacta situaciones que con palabras nos llevaría un amplio espacio explicar, pudiendo extenderse la definición para abarcar no sólo una función de onda para una partícula sino inclusive dos o más, como lo muestra el siguiente ejemplo:
en donde se lleva a cabo la evaluación de una esperanza matemática entre dos estados, siendo el primer estado el producto de dos funciones de onda A y B asignadas a la partícula 1 y a la partícula 2 respectivamente, y siendo el segundo estado el producto de las mismas dos funciones de onda A y B pero asignadas a la partícula 2 y a la partícula 1 respectivamente. Como debe serlo en base a la definición, para evaluar las integrales múltiples que nos representa esta expresión bra-ket debemos tomar el conjugado complejo de lo que va puesto del lado del bra, en este caso φA(1)φB(2).
PROBLEMA: Considérese el caso de una partícula en una caja confinada a moverse unidimensionalmente dentro de una caja de longitud L. Supóngase que la partícula se encuentra inicialmente en el estado fundamental (o estado basal). Súbitamente, una de las paredes es movida hacia afuera dándole a la longitud de la caja una dimensión igual a 3L. ¿Cuál es la probabilidad de que la partícula se encuentre en el estado fundamental en la nueva caja?
Identificando a la función de onda para una partícula en una caja de longitud L en el estado fundamental como ψ1(L) y a la función de onda para una partícula en una caja de longitud 3L en el estado fundamental como ψ1(3L), la probabilidad de que la partícula permanezca en el estado fundamental en la nueva caja después de haber tenido el mismo estado anteriormente está dada por:
En una entrada anterior ya habíamos obtenido las funciones de onda para una partícula encerrada en una caja moviéndose unidimensionalmente, y las funciones de onda para dicha partícula en el estado fundamental tanto en una caja de longitud L como en una caja de longitud 3L serán:
Tomando el producto interno de ambas funciones a lo largo de la longitud inicial L de la caja:
Simplificando un poco sacando las constantes fuera de la integral:
Con la finalidad de evaluar la integral, haremos uso de la siguiente identidad trigonométrica:
Llevando a cabo la integración, tomando los límites y evaluando, tenemos entonces lo siguiente para el producto interno de las dos funciones de onda:
El cuadrado de esta cantidad será entonces la probabilidad que estamos buscando:
La evaluación numérica de esta probabilidad nos dá un valor de 0.1282, o bien un 12.82% de probabilidad.