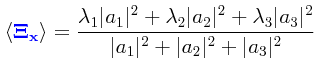Si a nivel sub-atómico el electrón es capaz de llevar a cabo un movimiento de precesión en torno al eje que representa las líneas de fuerza del campo magnético que le está siendo aplicado, entonces también debe desarrollar un movimiento rotatorio en torno al eje vertical, razón por la cual a la flecha que representa el spin del electrón como un vector se le dibuja frecuentemente posicionada a con la punta a lo largo de un cono, el cono que está siendo recorrido por el vector S:
Si la frecuencia angular de precesión del electrón se puede evaluar de alguna manera conociendo el campo magnético que está siendo aplicado, entonces se vuelve casi irresistible imaginar un experimento en el cual le aplicamos a los átomos una señal de radiofrecuencia que tenga el mismo valor que la frecuencia calculada de precesión para ver qué es lo que sucede, sintonizando la frecuencia que se le aplica al especimen bajo prueba al igual que como se sintoniza un radio hasta que se obtiene una respuesta al ocurrir el efecto de resonancia cuando la radiofrecuencia que está siendo aplicada es igual a la frecuencia de precesión. Esto se ha hecho, y ha llevado a cabo el desarrollo de una poderosa técnica de espectroscopía no-óptica conocida como la espectroscopía del spin electrónico (ESR, por sus siglas en inglés). Este efecto fue observado por vez primera en 1944, dando credibilidad a la hipótesis de que lo revelado por vez primera mediante el experimento Stern-Gerlach era realmente algo que tenía que ver con el spin del electrón idealizado como una especie de esfera con carga eléctrica girando sobre su propio eje.
Intrigados por los resultados obtenidos del experimento Stern-Gerlach, podemos intentar llevar a cabo otro tipo de experimento utilizando dos aparatos Stern-Gerlach en lugar de uno. El segundo aparato será posicionado en forma tal que el campo magnético inhomogéneo, en lugar de ser producido a lo largo del eje vertical, será producido a lo largo de un eje horizontal como se muestra a continuación:
El experimento que llevaremos a cabo ahora consistirá en mantener el aparato Stern-Gerlach inicial tal y como estaba, sin cambiarlo de posición. De este modo, seguiremos obteniendo dos haces de partículas que salen disparadas del primer aparato en direcciones opuestas. Pero ahora lanzaremos uno de esos haces hacia el segundo aparato Stern-Gerlach que está en posición “acostada” para ver qué es lo que sucede. Un experimento de este tipo, con dos aparatos Stern-Gerlach en lugar de uno, viene siendo un experimento Stern-Gerlach secuencial. En lo que llevaremos a cabo, construiremos dos aparatos Stern-Gerlach, uno con un campo magnético inhomogéneo fluyendo de un electroimán a otro a lo largo del eje vertical, el eje-z, que denominaremos SGz y el otro con un campo magnético inhomogéneo fluyendo de un electroimán a otro a lo largo del eje-x, que denominaremos SGx:
Como puede verse, el aparato SGz divide el haz de átomos de plata saliendo del horno en dos haces, el haz Sz+ y el haz Sz-. Por su parte, el aparato SGx divide el haz de átomos de plata saliendo del horno en los haces Sx+ y el haz Sx-.
El primer experimento Stern-Gerlach secuencial consiste en poner a la salida de un aparato SGz otro aparato SGz:
Como puede verse, la salida del segundo aparato SGz será un haz de átomos de plata Sz+, lo cual no es sorprendente porque se le alimentó con un haz de átomos de plata Sz+. No veremos átomos de plata Sz- saliendo del segundo aparato.
El segundo experimento Stern-Gerlach secuencial consiste en poner a la salida de un aparato SGz un aparato SGx:
Aquí sucede algo interesante. El segundo aparato toma el chorro de átomos de plata Sz+ que le está enviando el primer aparato, y nos proporciona dos haces, un haz de átomos de plata Sx+ y un haz de átomos de plata Sx-. Sin embargo, hemos destruído la información que poseíamos previamente acerca del valor del spin en el eje-z. Esto lo podemos confirmar unívocamente poniendo un tercer aparato, en este caso un aparato SGz, en cualquiera de las dos salidas del segundo aparato SGx. Hagámoslo poniendo el tercer aparato a la salida Sx+ del segundo aparato:
Como puede verse, el resultado de este último experimento resulta sorprendente. El primer aparato nos había separado los átomos de plata en dos haces y habíamos tomado el haz tipo Sz+ como entrada del segundo aparato. Tras esto, al tomar la salida tipo Sx+ del segundo aparato usándola para alimentar un aparato SGz, clásicamente esperaríamos obtener una confirmación de algo que esperaríamos obtener, un valor Sz+ para los átomos de plata. Y con esto, clásicamente, esperaríamos obtener el valor preciso del spin (positivo o negativo) en la dirección-z y también en la dirección-x, o sea en dos direcciones perpendicualres. Pero en lugar de que esto ocurra, el tercer aparato nos arroja tanto partículas del tipo Sz+ como partículas del tipo Sz-. Obviamente, algo ocurrió en el segundo aparato cuya interacción con el haz alteró la información que estaba saliendo del primer aparato. El ejemplo que acabamos de ver nos ilustra que no podemos determinar Sx y Sz simultáneamente. La selección hecha sobre el haz Sx+ que sale del segundo aparato destruye completamente cualquier información que teníamos acerca de Sz. Se trata, en efecto, de observables incompatibles que no pueden ser medidas simultáneamente. Esto es precisamente lo que nos reflejan las matrices de Pauli estudiadas previamente, las cuales no son conmutativas. Tomaremos nuevamente este tema con mayor detalle cuando tratemos el asunto en la entrada “El acto de medición”.
Clásicamente, si tenemos un trompo girando rápidamente, su momento angular L = (Lx, Ly, Lz) está dado por la fórmula L = Iω en donde I es el tensor momento de inercia y ω = (ωx, ωy, ωz) es la velocidad angular en torno al eje de giración. Observando qué tan rápido está girando el trompo, podemos determinar simultáneamente las tres componentes de ω. Si conocemos la forma geométrica del trompo y su densidad de masa, podemos calcular su momento de inercia. Con esto, no hay problema alguno en la determinación simultánea de las componentes del momento angular Lx y Lz para el trompo. Sin embargo, cualquier intento por hacer lo mismo en el mundo sub-microscópico fracasa rotundamente. La dificultad que enfrentamos al llevar a cabo este tipo de mediciones simultáneas en el mundo sub-microscópico no tiene nada que ver con la incompetencia del experimentador o con la precisión de sus aparatos, y por mucho que mejoremos nuestras técnicas experimentales no podremos hacer desaparecer la componente Sz- que sale del tercer aparato en el experimento secuencial de arriba.
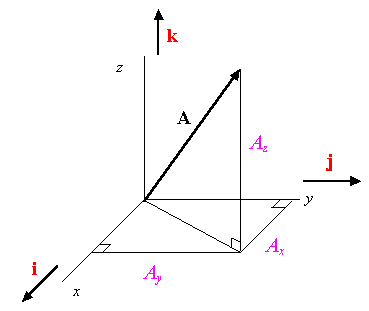
Si vamos a llevar a cabo un análisis mecánico-cuántico sobre el spin del electrón, no nos basta con saber lo que ocurre a lo largo de un simple eje coordenado. Necesitamos poder manejar de alguna manera la información relacionada con los tres ejes coordenados rectangulares Cartesianos. El problema es que la cantidad que describe los valores que puede tomar una esta cantidad física a lo largo de un eje coordenado está representado con una matriz y no mediante un simple número. Tenemos ya las tres matrices de Pauli que necesitamos para dar una representación cuántica al spin a lo largo de los tres ejes coordenados. El problema es, ¿cómo representamos vectorialmente algo cuyas componentes no son números sino matrices? Si se tratase de un avión en pleno vuelo, esto no representaría problema alguno, ya que podemos medir para el mismo una velocidad de 40 millas por hora de Norte a Sur, sumada a una velocidad lateral de 25 millas por hora de Este a Oeste, sumada a una velocidad de ascenso de 10 millas por hora suponiendo que el avión se esté elevando. Llamando A al vector velocidad del avión, las tres componentes representadas como (25,40,10), son las proyecciones del vector velocidad sobre cada uno de los ejes ortogonales:
Pero como ya se dijo, el problema que tenemos ahora es que los componentes del spin del electrón no son números, son matrices, las matrices de Pauli. Los ejes coordenados seguirán siendo los mismos, esto no cambiará:
La única forma en la cual podemos manejar esta situación que se nos presenta es definir al spin como un vector S cuyas componentes son matrices en lugar de números. Y las componentes que utilizaremos para ello serán precisamente las matrices de Pauli. De este modo tenemos la siguiente propuesta:
S = (Sx, Sy, Sz)
en donde:
PROBLEMA: (1) Obténganse las siguientes esperanzas matemáticas y dése una interpretación física a los resultados obtenidos:
(2) Obténganse las siguientes esperanzas matemáticas:
(3) Evalúese la siguiente expresión y dése una interpretación física al resultado obtenido:
Obtener la esperanza matemática de cualquier matriz requiere obtener primero los valores característicos eigen de dicha matriz (o una expresión de carácter general para los valores propios de la matriz) que nos permita aplicar las definiciones de la Estadística para poder obtener las esperanzas matemáticas a partir de dichos valores. Trabajando con la matriz Sx y usando como recurso intermedio un vector columna de dos componentes que denominaremos a = (a1,a2), el montaje matricial para obtener la ecuación característica que nos dará los valores eigen λ es el siguiente:
Ya hemos visto previamente cómo se resuelve un sistema de ecuaciones de este tipo. Llevando a cabo los procedimientos usuales, encontramos que la matriz Sx posee dos valores característicos:
Con estos dos valores característicos estamos en condiciones de poder evaluar las esperanzas matemáticas que estamos buscando para la matriz Sx. Repitiendo lo mismo para las matrices Sy y Sz encontramos que estas también tienen los mismos valores característicos λ1 y S2 que los de la matriz Sx.
(1) La evaluación de la esperanza matemática <Sx> de la matriz Sx es relativamente fácil de calcular, porque se trata simplemente de la media aritmética de los dos valores característicos de la matriz Sx:
Este resultado nos dice algo muy importante. Nos dice que, en promedio, habrá tantas partículas que posean un valor característico -ħ/2 como habrá partículas que posean un valor característico +ħ/2, nos dice que las probabilidades de obtener los resultados -ħ/2 y +ħ/2 están repartidas en partes iguales. Esto explica el por qué en un experimento Stern-Gerlach haya tantas partículas desviadas “hacia arriba” como habrá partículas desviadas “hacia abajo”. Naturalmente, al llevarse a cabo el experimento sobre una sola partícula, la partícula deberá tener necesariamente un solo valor definido, ya que la partícula sólo se podrá desviar “hacia arriba” o “hacia abajo”. ¿Y cómo podemos representar matricialmente al spin de una sola partícula cuyo valor bien definido simbolicemos como ξ? Lo hacemos mediante la matriz identidad I, multiplicándola por dicho valor. Manteniéndonos dentro de las representaciones matriciales de orden 2x2, esto lo escribiríamos como ξI. De este modo, tendríamos dos representaciones matriciales posibles de valores bien definidos:
Si suponemos que habíamos estado trabajando con una partícula con su spin descrito por la matriz Sx, la cual posee dos valores característicos con probabilidades iguales de ocurrencia, surge entonces una duda desde el punto de vista matricial: ¿cómo es que pasamos de una condición en la cual tenemos dos valores distintos, igualmente probables, a la condición en la cual tenemos únicamente uno de dichos valores? La respuesta, aunque no parezca obvia, radica en el acto de medición. Antes de llevar a cabo una medición sobre un sistema, todos los valores posibles eigen propios de la matriz del sistema son igualmente probables, podemos considerar que el sistema “existe” de alguna manera en cualquiera de dichos estados. Pero al momento de llevarse a cabo una medición para la detección de dichos estados, algo muy curioso sucede: el sistema se colapsa hacia uno de dichos estados:
Tras el colapso, ya no tenemos varios valores con cierta probabilidad de ocurrencia asignados a una misma partícula; se tiene un solo valor bien definido. Este proceso de colapso sigue siendo un asunto de mucha controversia y sigue siendo tema de debate y discusión en círculos filosóficos y científicos de prestigio. Evitaremos por lo pronto el andarnos quebrando la cabeza con cuestiones enigmáticas que no vienen al caso, y nos limitaremos a aceptar los resultados que nos dá la Mecánica Cuántica tal cuales.
(2) Para la evaluación de la esperanza matemática <Sx²> de la matriz Sx, basta con hacer extensiva la definición de la media cuadrática a los dos valores característicos de la matriz Sx, con lo cual obtenemos lo siguiente:
Las esperanzas matemáticas <Sx²> y <Sz²> obviamente serán las mismas que la que acabamos de obtener aquí por tratarse de los mismos valores característicos.
(3) Para la evaluación de:
podemos utilizar los resultados anteriores, a través de la relación:
Puesto que el valor <Sx> es igual a cero, obviamente <Sx>² también lo será, con lo cual el segundo término en la relación de arriba se vuelve cero, dejándonos únicamente con el primer término que ya evaluamos como ħ²/4. Entonces:
Podemos darle mayor claridad a esto último si extraemos la raíz cuadrada en ambos lados de la igualdad obteniendo así lo siguiente:
Lo que tenemos en el lado izquierdo de la igualdad lo podemos reconocer como algo que ya habíamos visto con anterioridad. Se trata de la incertidumbre que podemos esperar obtener en la procuración de un valor de Sx. En este caso, la incertidumbre es igual a ±.ħ/2. Puesto que el valor promedio que esperamos obtener en el laboratorio de las mediciones de Sx es igual a cero al ser <Sx> igual a cero, al ser la incertidumbre igual a ±.ħ/2 esto nos dice que el resultado de nuestra medición puede ser tan incierto en +ħ/2 unidades “hacia arriba” como en -+ħ/2 unidades “hacia abajo” antes de llevar a cabo la medición sobre una partícula individual. Naturalmente, al llevarse a cabo la medición, tiene lugar el proceso de colapso eliminándose la incertidumbre y obteniéndose una certeza. ¿Significa esto que ya burlamos las limitaciones impuestas por el principio de incertidumbre? La respuesta es un no rotundo, por el hecho de que las tres matrices Sx, Sy y Sz están interrelacionadas a través del principio de incertidumbre como consecuencia de las siguientes relaciones entre las matrices de Pauli (las cuales pueden ser verificadas fácilmente mediante multiplicaciones matriciales directas):
No es posible llevar a cabo una medición sobre Sx convirtiendo nuestra ignorancia sobre su valor en una certeza sin alterar cualquier conocimiento previo que hubiéramos tenido acerca de Sy y Sz. Una vez medido Sx, si procedemos a medir nuevamente Sx obtendremos el mismo valor una y otra vez, pero si tras ello procedemos a medir Sy entonces destruiremos la información que teníamos acerca de Sx y ahora Sx y Sz serán inciertos en la medida proporcionada por el principio de incertidumbre. En dondequiera que haya una relación descrita por un conmutador propio de las relaciones del conmutador de Born, habrá una incertidumbre a la cual será imposible escapar.
Hay seis relaciones de conmutación posibles para las matrices Sx, Sy y Sz usadas para representar los valores que puede tomar el spin del electrón. Si utilizamos números en lugar de letras para escribir los sub-índices que distinguen a cada matriz (S1, S2 y S3), estas relaciones de conmutación se pueden escribir de la siguiente manera:
PROBLEMA: Demostrar que:
S1S2 - S2S1 = [S1,S2] = iħS3
La solución de este problema se lleva a cabo mediante substituciones directas:
El utilizar sub-índices numéricos en lugar de letras para escribir las matrices utilizadas para representar al spin del electrón nos permite representar las seis relaciones posibles de conmutación de una manera compacta mediante la siguiente fórmula abreviada:
en donde el símbolo de permutación εijk (también conocido como el símbolo Levi-Civita o densidad Levi-Civita) se define de la siguiente manera:
El experimento Stern-Gerlach que se ha descrito con anterioridad permitió asignarle al electrón una cantidad llamada spin que explicó la separación de un haz de átomos de plata en dos haces distintos al ser pasado a través de un campo magnético no homogéneo, con los átomos repartidos en cada haz dependiendo del sentido en que el electrón estuviera girando sobre su propio eje. Esto tal vez hubiera sido el fin de la historia, excepto que no transcurrió mucho tiempo para que se llevaran a cabo otros experimentos en el cual se obtenían no dos bandas sino tres:
Aunque una explicación sencilla para la presencia de tres haces de partículas en lugar de dos podría consistir en suponer que además de poder girar en dos sentidos posibles sobre su propio eje de rotación el electrón puede permanecer totalmente “quieto”, resulta difícil aceptar la noción que algo tan móvil y tan dinámico como el electrón pueda estar realmente “quieto”. Esta hipótesis simplista fue desechada al hacer su aparición nuevas bandas espectrales, obligando a los teóricos a considerar que, además del spin del electrón, debía de haber otra cantidad originada no por el electrón girando sobre su propio eje sino por el electrón girando en torno al átomo, una cantidad adicional a la especificada por el nivel energético de cada órbita posible. A esta cantidad que ya no se le podía simbolizar como S se le simbolizó como L (la letra usada en la figura de arriba), el mismo símbolo utilizado para representar clásicamente el momento angular de un cuerpo girando en torno a otro. Habiendo tres valores posibles para L, las matrices de Pauli σ1, σ2 y σ3 ya no bastan para codificar los tres eigen-valores cuánticos posibles que podemos asignarle al momento angular orbital del electrón en sus componentes Sx, Sy y Sz; necesitamos otras tres matrices distintas (para poder asignar una componente matricial a cada coordenada) que posean cada una de ellas tres valores característicos. La pregunta ahora es: ¿existen tales matrices? Idealmente, se requiere que dichas matrices en caso de existir posean las mismas propiedades que las que poseen las matrices de Pauli para el spin del electrón, o sea anticonmutatividad (σ1σ2 = - σ2σ1), la propiedad de que cada matriz multiplicada por sí misma resulte en la matriz identidad (σ2² = I) y que el producto de cualquier par de dichas matrices produzca la tercera matriz multiplicada ya sea por +i o por -i. Felizmente, después de experimentar un poco resulta que sí es posible hallar tales matrices, las cuales identificaremos aquí con la letra griega “xi” minúscula (ξ) para no confundirlas con las matrices de Pauli:
Con estas matrices básicas tenemos entonces las siguientes matrices para un momento angular que puede tomar tres valores en lugar de dos, las cuales identificaremos con la letra griega “Xi” mayúscula (Ξ) :
Usando como recurso intermedio un vector columna de tres componentes que denominaremos a = (a1,a2,a1), el montaje matricial para obtener la ecuación característica que nos dará los valores eigen λ para la matriz Ξx es el siguiente:
Ξxa = λa
Resolviendo la ecuación característica, encontramos que los tres valores propios eigen de la matriz Ξx son:
Estos son los mismos valores propios que encontramos para las otras dos matrices Ξy y Ξz. Al igual que como lo hicimos en el caso del spin del electrón, también podemos tratar de evaluar aquí las siguientes esperanzas matemáticas:
Tentativamente, la primera esperanza matemática que vendría siendo evaluada sería la siguiente como un promedio aritmético:
Este procedimiento es válido siempre y cuando los eigenvalores λ1, λ2 y λ3 tengan la misma probabilidad de ocurrencia. Si cada uno de los eigenvalores tiene una probabilidad estadística de ocurrencia de un tercio, entonces el procedimiento que se acaba de dar es correcto. Sin embargo, si las probabilidades de ocurrencia están repartidas desigualmente, el simple promedio aritmético se nos cae, y tenemos que recurrir a una fórmula más elaborada como la siguiente:
En esta fórmula, correcta de acuerdo a lo que nos enseña la Estadística, |a1|² es la probabilidad de ocurrencia del eigenvalor λ1, |a2|² es la probabilidad de ocurrencia del eigenvalor λ2, y |a3|² es la probabilidad de ocurrencia del eigenvalor λ3. Con los tres eigenvalores de la matriz Ξx tendríamos entonces lo siguiente:
Del mismo modo, en vez de evaluar lo siguiente:
que sería lo correcto si las tres probabilidades de ocurrencia |a1|², |a2|² y |a3|² fuesen iguales, lo correcto (o más completo, incluyendo a la fórmula anterior como caso especial) vendría siendo:
PROBLEMA: Demostrar que la fórmula anterior se reduce a lo esperado cuando las tres probabilidades de ocurrencia para cada uno de los eigenvalores son iguales.
Si las tres probabilidades de ocurrencia están repartidas en partes iguales, entonces:
|a1|² = |a2|² = |a3|² = 1/3
De este modo:
Resulta claro que para poder evaluar las esperanzas matemáticas de una matriz en su forma correcta cuando las probabilidades de ocurrencia de sus eigen-valores son diferentes necesitamos conocer estas probabilidades de ocurrencia para cada uno de los eigenvalores.
¿Y de dónde vamos a sacar las probabilidades de ocurrencia para cada uno de los eigenvalores?
Respuesta: de la misma matriz.
Al resolver la ecuación característica de la matriz Ξx para encontrar sus autovalores propios eigen se utiliza un vector a que habíamos considerado como un mero artificio de ayuda. Pero resulta que este eigenvector, una vez normalizado a la unidad, es lo que nos proporciona las probabilidades de ocurrencia.
Toda la información que podamos conocer acerca de un sistema físico sub-microscópico está contenida en la matriz que describe la propiedad física que queramos evaluar para el sistema, siendo imposible poder extraer cualquier otra información adicional. Todo sale de la matriz. Cuando posteriormente nos adentremos al estudio de la Mecánica Ondulatoria, nos encontraremos con que toda la información que podamos conocer acerca de un sistema físico sub-microscópico está contenida en algo a lo cual en la Mecánica Cuántica se le conoce como la función de onda y que aquí podemos simbolizar como Ψ. Transferir un problema de la Mecánica Matricial a la Mecánica Ondulatoria o viceversa puede hacer más sencillo desde el punto de vista matemático el resolver el problema, pero no vamos a obtener más información que la que podamos obtener ya sea de la matriz o de la función de onda. En otros tiempos, ya superados, había quienes creían que era posible construír las matrices de modo tal que fuese posible eliminar las incertidumbres teóricas volviendo al universo determinista y mecanístico de Newton en donde todo era predecible a cualquier nivel. Si es posible tal cosa, hasta la fecha nadie ha logrado encontrar la forma de hacerlo.
Las probabilidades de ocurrencia |a1|², |a2|², |a3|² ... etc. para cada uno de los eigenvalores λ1, λ2, λ3 ... etc. tienen un impacto directo en las estimaciones de las intensidades de las líneas espectrales para los espectros de emisión de los elementos. Si la probabilidad de ocurrencia asociada con cierto nivel de energía para cierta línea del espectro es el doble de la probabilidad de ocurrencia para otro nivel de energía de otra línea del espectro del mismo elemento, entonces la intensidad de dicha línea registrada por el espectrómetro deberá ser dos veces mayor. Esto ya es algo que el modelo atómico planetario de Bohr era incapaz de predecir. En el caso del experimento Stern-Gerlach, numerosos experimentos han confirmado que ambas “bandas”, tanto la que corresponde a los átomos de plata con el spin de su electrón apuntando “hacia arriba”, como la que corresponde a los átomos de plata con el spin de su electrón apuntando “hacia abajo”, tienen la misma intensidad.
Si definimos al vector a como un vector columna a, y usándolo como referencia definimos al vector renglón a* siendo los componentes de este último los conjugados complejos de los componentes respectivos del vector renglón a, podemos escribir la versión matricial de la esperanza matemática <Ξx> de la matriz Ξx del modo siguiente:
El lector se debe convencer a sí mismo de que el resultado de estas últimas evaluaciones nos resulta no en una matriz sino en un número. En el denominador, la operación matricial a*a es el equivalente pleno del producto escalar de dos vectores:
mientras que en el numerador la operación Ξxa nos producirá un vector columna que multiplicado con el vector renglón a* nos producirá también un escalar, un número. Vale la pena recordar bien esta última fórmula, porque cuando veamos la evaluación de la esperanza matemática en la Mecánica Ondulatoria nos encontraremos con algo muy parecido, excepto que tanto en el numerador como en el denominador tendremos unas integrales en lugar de unas operaciones matriciales siendo el denominador algo que se conoce en la Mecánica Ondulatoria como la condición de normalización. En el caso que estamos estudiando aquí, la condición de normalización escrita tanto en su forma algebraica ordinaria como en su forma matricial viene siendo la siguiente:
Puesto que un vector renglón a, considerado como una matriz 1xn (una matriz que consta de un solo renglón y de n columnas) puede ser tomado como la transpuesta de un vector columna aT que a su vez puede ser considerado como una matriz nx1 (una matriz que consta de n renglones y de una sola columna), la operación matricial a*a en realidad es el producto de un vector a y el conjugado complejo de su transpuesta a* (o bien, la transpuesta de su conjugado complejo). El producto de ambos, por la forma en que ha sido definido, siempre será igual a un número real y positivo (nunca negativo), que es justo lo que necesitamos para poder representar cantidades físicas medidas en el laboratorio. Y cuando el producto está normalizado a la unidad, podemos utilizarlo para darle una interpretación acorde con la probabilidad estadística tal y como lo hemos hecho arriba. Esto significa que un vector (de cualquier dimensión) cuya “longitud” haya sido normalizada a la unidad (extendiendo el alcande del teorema de Pitágoras como sea necesario) puede ser considerado como un vector de probabilidad, siempre y cuando vaya asociado con una matriz de dimensión compatible para que se pueda llevar a cabo una operación matricial como a*Ξxa.
PROBLEMA: Generalmente hablando, la división entre dos matrices A y B:
no está definida. Sin embargo, hay ciertos casos especiales en los cuales a este cociente se le puede dar una definición. Considérse el siguiente cociente:
en donde I es una matriz identidad 2x2, a0 es un número real, a es un vector tridimensional con componentes reales y σ es un vector de matrices cuyas tres componentes son las matrices de Pauli, o sea:
(1) Demuéstrese la forma en la cual se le podría dar una definición al cociente matricial proporcionado. (2) Obténgase el determinante tanto de la expresión matricial A del numerador como de la expresión matricial B del denominador.
(1) La forma más directa para tratar de darle una interpretación al cociente matricial proporcionado consiste en tomar la expresión matricial del denominador escribiéndola como una matriz inversa, o sea:
De este modo, el cociente matricial A/B quedaría definido como AB-1, de forma tal que para obtener el cociente matricial obtendríamos primero la inversa de la matriz B, tras lo cual pre-multiplicaríamos el resultado con la matriz A.
La evaluación directa de la expresión matricial A en el numerador mediante operaciones matriciales elementales es la siguiente:
Por otro lado, la evaluación directa de la expresión matricial B en el denominador mediante operaciones matriciales elementales es la siguiente:
Si comparamos las matrices A y B ya evaluadas, podemos verificar fácilmente que podemos obtener la matriz B en el denominador tomando primero la transpuesta de la matriz A y tomando tras esto el conjugado complejo de los elementos de la matriz resultante (o bien, tomando primero el conjugado complejo de los elementos de la matriz A, y tras esto tomando la transpuesta de la matriz resultante, el resultado viene siendo el mismo). De este modo, el cociente matricial A/B se puede escribir como:
Obsérvese que en el último paso hemos escrito a la matriz del denominador (antes de tomarse el inverso de la matriz) como la transpuesta del conjugado complejo de la matriz en el numerador, para lo cual utilizamos el símbolo daga como exponente.
Puesto que A es una matriz 2x2, y la inversa de la transpuesta de su conjugado complejo también debe ser una matriz 2x2, el producto A(A†)-1 será una matriz 2x2, y de esta manera el resultado del cociente matricial quedará también definido.
En la forma en la cual se ha definido el cociente matricial A/B como AB-1 hay una ambigüedad, ya que así como fue definido llevando a cabo la pre-multiplicación de B-1 por A, del mismo modo podríamos haberlo definido llevando a cabo la post-multiplicación de B-1 por A, o sea formando el producto B-1A. Para que no haya ambigüedad alguna, se requiere que el resultado que se obtenga sea el mismo ya sea con una pre-multiplicación o con una post-multiplicación, o sea:
(2) Habiendo obtenido las matrices A y B en forma explícita, los determinantes respectivos resultan ser los siguientes empezando por el determinante de la matriz en el numerador:
seguida por la evaluación del determinante de la matriz en el denominador:
Obsérvese un hecho interesante: los determinantes de ambas expresiones matriciales A y B terminan evaluados como lo mismo. Esto nos dá una pista adicional sobre otras simplificaciones y manipulaciones que se pueden llevar a cabo aquí sobre el cociente matricial original, incluso la posibilidad de remover la ambigüedad que se había mencionado anteriormente en caso de que sea posible demostrar que A(A†)-1 dará el mismo resultado que (A†)-1A.