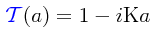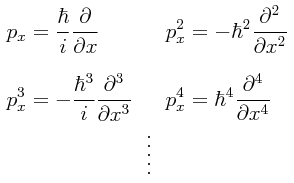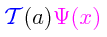x’ = x + a
y’ = y + b
z’ = z + c
haciéndose algo similar en el caso de la variable del tiempo:
t’ = t0 + Δt
Un ejemplo sencillo consistiría en tomar al círculo centrado en el origen:
cuya ecuación en coordenadas rectangulares Cartesianas es:
y desplazarlo a una distancia R.=.(a,b) con respecto a su posición original mediante la transformación:
obteniendo así el mismo círculo trasladado espacialmente:
y cuya nueva ecuación en coordenadas Cartesianas es:
Sin embargo, esta simple prescripción para llevar a cabo el desplazamiento espacial de una función de onda está condenada al fracaso no sólo porque la función de onda Ψ, como hemos visto, puede estar dada por una expresión que contenga cantidades imaginarias o complejas, sino por el hecho de que es el cuadrado de la función de onda, o sea |Ψ|2, lo que nos dá la probabilidad de encontrar a la partícula en cierta región del espacio tridimensional.
Habiendo visto con anterioridad que prácticamente todo lo que tiene que ver con la función de onda Ψ requiere el uso de operadores que actúan de alguna manera multiplicativa sobre la función de onda, ¿por qué habrían de ser diferentes las operaciones de desplazamiento espacial o temporal? Estas consideraciones nos llevan a concluír que el esquema simplista que vimos al principio pasa por alto el hecho de que cuando tenemos una función de onda Ψ(r,t) lo que se requiere para llevar a cabo una operación de desplazamiento espacial es un operador de traslación espacial que actúe sobre la función de onda, produciendo una nueva función de onda desplazada Ψ(r’,t). Y del mismo modo, si lo que se require es llevar a cabo una operación de desplazamiento temporal sobre una función de onda, también debe de existir un operador de desplazamiento temporal que actúe sobre la función de onda produciendo el efecto del paso del tiempo sobre una función de onda. Suponemos que este tipo de operadores de desplazamiento espacial y temporal deben existir siempre y cuando puedan ser definidos de una manera correcta que funcione. ¿Pero qué podremos utilizar como guía para la especificación de estos operadores?
“Congelando” la variable del tiempo para fines de simplicidad, empezaremos por suponer que es factible construír un operador de traslación que sea capaz de desplazar espacialmente una función de onda en una distancia a, al cual representaremos de la siguiente manera:
La aplicación (operacionalmente multiplicativa) de este operador de traslación sobre una función de onda Ψ(x) debe producir una nueva función de onda Ψ(x+a):
Esto mismo, expresado en notación bra-ket de Dirac, se escribe de la siguiente manera:
En lo anterior, se ha supuesto implícitamente que el desplazamiento se está llevando a cabo en una sola dimensión en la dirección positiva del eje-x. Pero no es necesario estar limitados a una sola dimensión; el desplazamiento se puede llevar a cabo también en tres dimensiones, en cuyo caso el eigenket de posición estará referenciado a un vector x, en cuyo caso el efecto de la aplicación del operador de traslación sobre un eigenket de posición tridimensional se puede expresar de la siguiente manera en notación bra-ket:
Hay que poner atención cuidadosa en esto último y en el hecho de que no es una ecuación eigen. No puede serlo, ya que un desplazamiento traslacional en cierta dirección no puede dejar a una función de onda Ψ en la misma posición que la que tenía antes de llevarse a cabo el desplazamiento. (Sin embargo, si el desplazamiento no es un moviento de traslación en cierta dirección sino una rotación, definitivamente sí es posible que la función de onda pueda quedar exactamente en la misma posición que la que tenía antes de llevarse a cabo la rotación, lo cual a su vez tendrá implicaciones profundas ya que a través de rotaciones es posible anticipar que se podrán tener operadores de rotación que al ser aplicados sobre cierta función de onda Ψ -o sobre cierto eigenket, que es lo mismo- la girarán haciéndola regresar a su posición original, lo cual implica que será posible tener ecuaciones eigen mediante operaciones de rotación, lo cual a su vez nos llevará inevitablemente a la “extraña ecuación de Born” al estar asociadas las rotaciones con el momento angular.)
Otro hecho trascendental que no debe perderse de vista es que el ket de posición representa una variable continua que no está sujeta a discretización alguna. Podemos fijar límites al espacio físico en el cual se lleva a cabo un fenómeno de naturaleza cuántica, como lo hacemos en el caso de una partícula encerrada dentro de una caja unidimensional a la cual le asignamos una longitud L, pero el espacio en sí comprendido dentro de la caja no está sujeto a ninguna discretización, ya que en principio y conceptualmente ese espacio unidimensional puede ser subdividido hasta el infinito. Esta conceptualización siempre conlleva el riesgo, desde luego, de que una nueva teoría sobre la naturaleza del espacio-tiempo pueda poner un límite absoluto a la subdivisión de un espacio físico (en cuyo caso el intervalo espacial entre dos puntos en vez de poderse corresponder en una relación bi-unívoca de uno a uno con un sub-conjunto del conjunto de los números reales se correspondería con un sub-conjunto de los números enteros). Sin embargo, a estas alturas, no hay razón para meternos en complejidades filosóficas y matemáticas que sólo desviarán la atención de las ideas que estamos intentando desarrollar.
Al igual que como lo hemos visto previamente con otros operadores como el operador Hamiltoniano de energía H, el operador de traslación es algo que siempre actúa sobre lo que está a su derecha. Esto implica que si hacemos un compuesto de varios operadores de traslación, el primer operador que actúa sobre la funcion de onda Ψ es el que está más a la derecha de los operadores, tras lo cual el siguiente operador en actuar sobre la función de onda trasladada es el operador que estaba a la izquierda del primer operador, y así sucesivamente:
Aunque tratándose de operadores de traslación, el orden en el cual sean aplicados sobre la función de onda Ψ no tiene mayor trascendencia, esto ya no será válido cuando entremos de lleno al tema de los operadores de rotación en donde la no-conmutatividad es la regla del juego. Con la finalidad de evitar confusiones a medida que la notación vaya creciendo en complejidad, se mantendrá vigente todo el tiempo la prescripción de que los operadores sucesivos múltiples se deben ir escribiendo de derecha a izquierda siguiendo el orden en el cual irán actuando uno tras otro sobre la función de onda.
Habiendo definido al operador de traslación, el siguiente paso consiste en fijar las “reglas del juego”. Tenemos que dejar en claro de antemano cuáles son las propiedades que debe cumplir el operador de traslación, propiedades que en caso de no cumplirse servirán para desechar los operadores de traslación que sean considerados como posibles candidatos.
La primera propiedad que debe cumplir el operador de traslación, la más esencial, la más básica, es que cuando el desplazamiento espacial a que produce sobre una función de onda Ψ se aproxima a cero el efecto sobre la función de onda en la cual actúa debe ser tal que la función de onda venga quedando en la misma posición. En efecto, estamos requiriendo que para un desplazamiento espacial igual a cero el operador de traslación se convierta en un operador identidad:
En este caso, el operador identidad lo podemos tomar simplemente como el número 1. Sin embargo, podemos dejar abierta la posibilidad de que el operador de traslación pueda ser un operador matricial, en cuyo caso la condición anterior estipula que al reducirse a a cero el operador de traslación se debe convertir en la matriz identidad:
¿Significa esto que estamos trabajando ya en el ámbito de la Mecánica Matricial? Desde luego que no, porque este operador de traslación es un operador que actúa sobre una función de onda Ψ. En la Mecánica Matricial, o hablando en términos más generales, en lo que se conoce como la representación de Heisenberg, no hay función de onda alguna que resienta el efecto de un operador de traslación aplicado sobre la función de onda; lo que cambia son las componentes de una matriz, la matriz que describe al sistema físico bajo consideración. Aquí lo que es objeto de modificaciones es la función de onda Ψ sobre la cual actúa el operador de traslación, en lo que se conoce como la representación de Schrödinger. Sin embargo, ello no significa que no podamos considerar la posibilidad de postular otra clase de operadores de traslación en los cuales la función de onda Ψ permanezca intacta pero que sea el operador de traslación el que cambie, lo cual nos abre un nuevo horizonte de posibilidades. Dejaremos por lo pronto pendiente este asunto para no distraernos de nuestro objetivo central que es el definir un operador de traslación que nos pueda ser útil dentro de la Mecánica Ondulatoria.
La segunda propiedad del operador de traslación, también esencial y básica, es que debe ser posible aplicar dos o más operadores de traslación en sucesión (uno tras otro) sobre una función de onda Ψ(x), y el efecto resultante debe ser obtenible mediante la aplicación de una sola operación de traslación:
Esto es evidente. Si se aplica un desplazamiento a1 de 1 milímetro en cierta dirección, seguido de otro desplazamiento a2 de 2 milímetros en la misma dirección, el efecto que se obtiene debe ser el mismo que el que se obtenga aplicando un desplazamiento a1+a2 de 3 milímetros en la misma dirección.
La tercera propiedad que se debe de cumplir en todo momento al usar operadores de traslación es que los operadores de traslación deben ser conmutativos. En efecto, si se aplica primero un desplazamiento a1 de 1 milímetro en cierta dirección, seguido de otro desplazamiento a2 de 2 milímetros en la misma dirección, el efecto que se obtenga sobre la función de onda Ψ(x) debe ser el mismo que si se aplica primero un desplazamiento a2 de 2 milímetros en cierta dirección, seguido de otro desplazamiento a1 de 1 milímetro en la misma dirección:
Hasta aquí hemos considerado operadores de traslación que actúan unidimensionalmente, moviendo a la función de onda sobre el eje-x. Pero igual podemos postular un operador de traslación bi-dimensional que sea capaz de desplazar una función de onda Ψ(x) en cualquier dirección sobre un plano. O podemos ir hasta la situación física real postulando un operador de traslación que pueda desplazar una función de onda tri-dimensional Ψ(r) en cualquier dirección de un espacio tri-dimensional, especificando por separado como un vector de desplazamiento x = (a,b,c) las magnitudes de los desplazamientos ortogonales (a ángulos rectos) en un sistema de ejes coordenados Cartesianos:
La acción de este operador de traslación tridimensional es la siguiente:
Y una cosa que destaca de inmediato es que las traslaciones sucesivas en direcciones diferentes (por ejemplo, el eje-x y el eje-y) conmutan, . Podemos ver esto con mayor claridad en la siguiente figura en la cual se tienen dos recorridos diferentes, uno de color verde y el otro de color magenta, y no importa cuál de los dos recorridos se tome el resultado final será el mismo:
Regresando al caso especial unidimensional para mantener las cosas simples, de lo anterior se deduce que los operadores de traslación deben cumplir necesariamente con la propiedad asociativa.
Otra propiedad que aquí puede parecer trivial pero que no lo será tanto al momento de resolver problemas que involucren otros tipos de operadores es que debe ser posible invertir cualquier operación de desplazamiento aplicando un desplazamiento de la misma magnitud pero en la dirección contraria. Puesto de otra manera, debe existir un operador inverso de traslación. A continuación se muestra del lado izquierdo de la igualdad la representación simbólica del operador de traslación inverso utilizando el exponente -1 que se acostumbra utilizar (sin que ello implique ni remotamente hablando una operación aritmética de inversión como ocurre cuando se trabaja con números), mostrándose del lado derecho de la igualdad que esta operación de inversión de traslación se debe poder llevar a cabo con un operador de traslación en el cual se le ha invertido el signo a la magnitud del desplazamiento:
Las propiedades dadas arriba son las que debe cumplir el operador de desplazamiento espacial que estamos buscando. A tales propiedades debemos agregar otra que veremos más abajo.
Sin duda alguna, la característica principal que distinguirá al operador de traslación que estamos tratando de construír es que el producto sucesivo de dos operadores de traslación (uno de ellos aplicando un desplazamiento espacial a1 y el otro aplicando un desplazamiento espacial a2 a la función de onda ó ket) deberá ser combinado de modo tal que la traslación equivalente única se lleve a cabo sobre una distancia a1+a2. En pocas palabras, se requiere equipar notacionalmente un producto operacional con una suma, ya que como puede verse:
si ignoramos a la función de onda y nos enfocamos directamente sobre el aspecto operacional, es obvio que:
La única función matemática que cumple este requerimiento, la única función matemática capaz de llevar esto a cabo es la función exponencial (esta es la razón por la cual en otros tiempos en los que no había calculadoras de bolsillo y mucho menos computadoras personales de escritorio se recurría a las tablas de logaritmos y a las hoy obsoletas reglas de cálculo, ya que permitían efectuar multiplicaciones y divisiones mediante simples sumas y restas, habido el hecho de que los logaritmos, basados a su vez en la función exponencial tienen tal propiedad):
Esto nos sugiere que el operador de traslación tiene que tener un aspecto como el siguiente:
Queda, desde luego, la posibilidad de que a este operador de traslación vaya anexado como multiplicador un factor de fase eφ similar al ángulo de fase φ que usualmente aparece como un apéndice en la solución general de las ecuaciones de onda. Sin embargo, este factor de fase se toma como irrelevante, ya que no hay significado físico alguno que se le pueda adscribir a la fase de una función de onda (el valor calculado de una observable no puede depender de un valor particular de la fase). Es por ello que usualmente se toma eφ como igual a la unidad:
El “esqueleto” del operador de traslación que estamos construyendo parece irse acercando a su forma ideal con las propiedades que le exigimos que tenga. Sin embargo, falta tomar en cuenta un detalle importante: la conservación de la probabilidad. Es razonable esperar que si un ket general de posición |ξ> está normalizado a la unidad:
el ket trasladado también estará normalizado a la unidad:
Tomando un ket general de posición:
y obteniendo de lo anterior la expresión que le es dual, o sea el bra general de posición que está siendo actuado por el conjugado complejo del operador de traslación:
entonces, trabajando “hacia atrás”, vemos que:
Para que esto último sea cierto, se requiere que:
En palabras, se requiere que el operador de traslación sea unitario, y esto requiere que el conjugado complejo del operador de traslación sea también el operador inverso del operador de traslación. Esta característica muy especial de unitaridad es lo que motiva a representar al inverso del operador de traslación con un símbolo alterno en el cual se le agrega una daga como super-índice en lugar del exponente -1:
Y llegamos así a la propiedad que nos faltaba de agregar a la lista de las propiedades que debe satisfacer el operador de traslación: se requiere que el operador de traslación multiplicado por su conjugado complejo produzca un operador identidad. Pero el operador exponencial que hemos estado investigando arriba no es capaz de hacer tal cosa, ya que:
Inevitablemente, tenemos que introducir el número imaginario i como un factor en el exponente del operador de traslación, con lo cual se puede satisfacer la condición de que el operador de traslación sea unitario:
Tenemos ya una buena idea sobre el tipo de operador de traslación que estamos buscando. Sin embargo, el procedimiento anterior, intuitivo, no nos revela la forma matemática exacta del operador de traslación. Una posibilidad, la más sencilla posible, es la que veremos a continuación.
PROBLEMA: Demuéstrese que, si se supone que el desplazamiento espacial de una función de onda se lleva a cabo sobre una distancia tan pequeña que esta distancia puede ser considerada casi como un desplazamiento infinitesimal, la siguiente expresión para el operador de traslación:
en la cual la cantidad K es Hermitiana cumple con todas las propiedades que esperamos que tenga un operador de desplazamiento espacial.
Trabajaremos sobre la base de que el desplazamiento espacial es tan pequeño que casi puede tomarse como un desplazamiento infinitesimal:
Para el operador de traslación proporcionado, la primera propiedad ciertamente se cumple, ya que cuando el desplazamiento espacial a que se produce sobre una función de onda Ψ se aproxima a cero el operador de traslación se convierte en un operador identidad:
La segunda propiedad del operador de traslación, según la cual debe ser posible aplicar dos o más operadores de traslación en sucesión (uno tras otro) sobre una función de onda Ψ(x), siendo el efecto resultante obtenible también mediante la aplicación de una sola operación de traslación, también se cumple, si despreciamos el término de segundo orden (lo cual es válido habido el hecho de que se supone que a es casi infinitesimalmente pequeño):
Dos operadores de traslación definidos de la manera propuesta también cumplen con la propiedad de que la aplicación de los operadores sea conmutativa:
Igualmente, se cumple la propiedad asociativa cuando se tienen tres operadores de traslación:
Si estamos dispuestos a despreciar el término de segundo orden, podemos comprobar que el operador de traslación también tiene su inverso que revierte un desplazamiento espacial en un sentido con otro desplazamiento de la misma magnitud pero en dirección contraria:
Notacionalmente, esto implica que:
Ahora bien, suponiendo que la cantidad K es Hermitiana (lo cual requiere que el conjugado complejo de la misma K* sea igual a dicha cantidad K, o sea que K*.=.K) el conjugado complejo del operador de traslación espacial propuesto en el enunciado del problema es:
Por lo tanto, se tiene también para este operador que el operador inverso es igual al conjugado complejo del operador:
El operador indudablemente es unitario, ya que si tomamos el producto del operador con su conjugado complejo y despreciamos términos de segundo orden en a, se obtiene el operador identidad:
El operador es, por lo tanto, un operador unitario, cumpliendo entonces con todas las propiedades que hemos fijado para un operador de traslación. Luego el operador propuesto en este problema es un operador de traslación válido para desplazamientos muy pequeños.
Aceptando al operador 1-iKa como un operador de traslación válido, estamos en condiciones de poder obtener una relación fundamental entre K y a. Obsérvese por un lado que:
en donde en la primera línea al lado izquierdo de la igualdad se tiene a un operador posición actuando sobre un operador de traslación que a su vez está actuando sobre un eigenket de posición, dando como resultado (en la primera línea, como consecuencia de la acción del operador de traslación) un eigenket trasladado; mientras que en la segunda línea como resultado del operador de posición actuando sobre un eigenket de posición trasladado (en la primera línea) se produce en virtud de la eigenecuación el eigenvalor que multiplica al eigenket de posición. Invirtiendo el orden de los operadores (posición y traslación) que actúan sobre el ket de posición, se tiene por otro lado:
en donde en la segunda línea se tiene al eigenvalor de la posición como resultado del operador posición actuando (en la primera línea) sobre el eigenket de posición, eigenvalor que por ser una observable física conmuta con el operador de traslación, el cual actúa sobre el eigenket de posición trasladándolo (cuarta línea). Usando los dos resultados obtenidos, si formamos un conmutador de Born con el operador posición y con el operador de traslación, haciendo actuar al conmutador sobre un eigenket de posición, se tiene:
o bien:
Usando el operador de traslación 1-iKa en esto, se obtiene:
Esto nos confirma que tanto x como K son operadores, ya que si cualquiera de ellos fuera una simple constante numérica el resultado del conmutador sería cero en lugar de i. Lo anterior supone un desplazamiento espacial unidimensional llevado a cabo por un operador de traslación unidimensional. Generalizando esto a un espacio de tres dimensiones en el sistema de coordenadas rectangulares Cartesianas, se puede escribir lo siguiente con la ayuda del δ de Kronecker:
Esta expresión nos define la relación que hay entre los tres operadores de posición y los tres operadores K respectivos.
No se ha definido aún la naturaleza del operador K que sirve para definir a su vez al operador de traslación. En virtud del número 1 que aparece en el primer término, carente de dimensiones en algún sistema de unidades, el segundo término en:
también debe ser adimensional. Careciendo el número imaginario i de dimensión alguna en un sistema de unidades, y siendo a una longitud (medida en metros, centímetros, etc.), esto impone el requerimiento de que K esté medido en unidades inversas de longitud (metro-1, cm-1, etc.). Y si el operador de traslación ha de ser un verdadero operador mecánico-cuántico, esperamos que K incorpore de alguna manera la constante reducida de Planck ħ. Esto nos motiva a recurrir a la relación de De Broglie que relaciona en una sola expresión la dualidad onda-partícula de la materia, para ver la forma en la cual podemos determinar la naturaleza de K:
Una forma alterna en la cual se puede expresar la relación de De Broglie es la siguiente en donde se sustituye la constante de Planck h por la constante reducida de Planck ħ:
La cantidad 2π/λ posiblemente le resulte familiar al lector. Es el número de onda, frecuentemente representado como k. Y está expresado precisamente las dimensiones de unidades inversas de longitud (metro-1, cm-1, etc.). De este modo, se tiene:
Esto se puede manifestar en un espacio tridimensional sobre un sistema de coordenadas Cartesianas rectangulares en forma vectorial de la siguiente manera:
Lo anterior también se puede expresar como (obsérvese que el vector de onda k tiene la misma dirección que el momentum p en virtud de ser ħ una simple constante numérica):
Como ya se señaló, el número de onda k está expresado precisamente en unidades inversas de longitud, al igual que su generalización tridimensional vectorial k. Limitándonos a trabajar sobre el eje-x como lo hemos estado haciendo por simplicidad, y tomando tanto el número de onda kx como el momentum px sobre el eje-x, se vuelve factible substituír a la cantidad K en el operador de traslación por kx, substituyendo subsecuentemente a kx por px dividido entre ħ:
Esto último, válido para desplazamientos a muy pequeños, nos revela algo muy interesante. Puesto que tanto a como ħ son cantidades físicas que pueden considerarse fijas, lo que realmente nos está generando la traslación es el operador del momentum px, un resultado que concuerda con la misma conclusión a la cual se llega mediante la física clásica: el operador del momentum es el generador de los desplazamientos espaciales.
Ahora echaremos mano del resultado obtenido previamente:
En tres dimensiones, conociendo ya la relación que existe entre cada operador Kj y la componente respectiva pj del momentum, podemos escribir la siguiente relación fundamental:
Esta conclusión es de importancia fundamental. Hemos obtenido la “extraña ecuación” de Max Born. Y la hemos obtenido sin recurrir en lo absoluto a ninguna de las matrices que se utilizan en la Mecánica Matricial, siendo por lo tanto el resultado cien por ciento válido dentro la Mecánica Ondulatoria.
Podemos ir más lejos con lo que hemos obtenido. Para ello, recurriremos al operador identidad (conocido también como la relación de completitud o cerradura) para el caso continuo (véase la entrada titulada “El espacio de Hilbert II”):
A continuación, se aplicará al operador de traslación sobre un ket general de estado, injertando primero al operador identidad y tras ello ejerciendo la acción del operador sobre el ket que está situado a su derecha:
Si efectuamos las siguientes substituciones (recuérdese que a representa un desplazamiento fijo, constante):
entonces lo siguiente debe ser cierto:
Pero de hecho esto más que una implicación es una igualdad, ambas relaciones son iguales, ya que la integración es llevada a cabo sobre todo el espacio (desde -∞ hasta +∞) y la variable (posición) de la integración se elimina al llevarse a cabo la integración entre los límites. Es como si se llevara a cabo la integración de un “pulso de onda rectangular”, no importa si el pulso de onda es relocalizado (trasladado) en una cantidad finita a en cierta dirección, al llevarse a cabo la integración desde -∞ hasta +∞ el resultado de la integración será exactamente el mismo. Usando entonces:
se tiene:
Puesto que:
entonces:
Reemplazando ahora (en el lado izquierdo de la igualdad) al operador de traslación que está actuando sobre el ket general de estado por el operador de traslación casi infinitesimal que tenemos arriba:
Comparando ambos lados de la igualdad, resulta obvio por la presencia del factor a que el segundo término al lado izquierdo de la igualdad debe ser igual al segundo término en el lado derecho de la igualdad, y si igualamos ambas cantidades de hecho a se elimina:
Podemos pre-multiplicar ambos miembros de lo anterior por un bra general de estado de la siguiente manera:
Si hacemos las siguientes identificaciones:
mediante las cuales se hace definida a una función de onda ψα como una función de onda cualquiera en el espacio-posición, y como ψβ* al conjugado complejo de otra función de onda también en el espacio-posición, entonces la relación se convierte en lo siguiente:
Esta relación nos debe resultar familiar, ya que es la esperanza matemática del operador px tomada entre los dos estados α y β, justo en el orden de términos que hemos estado utilizando desde un principio. Pero lo más importante es que nos dice que el operador del momentum px está dado por:
Destaca el hecho de que esto no es algo que hayamos utilizado como punto de partida en el análisis que se ha llevado a cabo. No es un postulado. Se trata más bien de algo que hemos derivado a partir de la propiedad mecánico-cuántica del momentum como el generador de traslaciones.
El operador de traslación que tenemos en nuestras manos es válido para desplazamientos muy pequeños, casi infinitesimales. Pero aún considerando que las dimensiones físicas típicas de los fenómenos propios de la Mecánica Cuántica son bastante pequeñas (del orden de los Angstroms o inclusive más pequeñas aún) estamos interesados en saber lo que sucede tratándose de desplazamientos finitos medibles a escala macroscópica con aparatos de laboratorio. ¿Cómo podemos manejar esta situación? La respuesta consiste en que si a un desplazamiento pequeño, casi infinitesimal, le aplicamos otro desplazamiento igualmente pequeño, seguido de otro y muchos más, eventualmente tendremos un producto formado por una cantidad bastante grande de operadores de traslación que en conjunto equivaldrán a una traslación finita que de pequeño no tendrá nada. La pregunta ahora es: ¿puede expresarse esto en una forma exponencial, que según lo que vimos arriba, es la forma a la que eventualmente queremos llegar? Para responder a esto en forma adecuada, tenemos que repasar una manera alterna de obtener el número e (aproximadamente igual a 2.718281) que es algo distinta a la expansión usual en series de Taylor:
Entre más grande sea el número n, tanto mejor será la aproxiamación hecha con esta relación al número e. A continuación se dan los resultados de la evaluación para valores de n iguales a 3, 50 y 100:
Como puede verse, la aproximación va mejorando y el error que se comete en la evaluación de e va disminuyendo conforme aumenta el valor de n. Aceptando como válida la relación anterior, puede demostrarse mediante la inducción matemática la siguiente generalización de lo anterior:
Tomando en consideración esto último, el operador de traslación compuesto puede ser construído de la siguiente manera como el producto creciente de una cantidad cada vez mayor de factores (obsérvese que dentro de cada factor la cantidad a va disminuyendo conforme aumenta n, pero el producto sucesivo creciente se encarga de amortiguar la disminución de a):
En el límite conforme n.→.∞, se debe tener entonces, con exactitud matemática:
En el lado derecho de la igualdad se tiene justo el operador de traslación que estábamos buscando.
El operador de traslación de la Mecánica Ondulatoria es entonces, confirmando que el operador del momentum es el generador de traslaciones:
Este resultado parece elemental, sin chiste, no parece ser gran cosa, hasta que tomamos en cuenta el hecho de que el momentum px es el operador diferencial que hemos estado usando con antelación:
Y puesto que kx es igual al operador diferencial px dividido entre ħ, se deduce nuevamente que la cantidad K de la que se hablaba en el operador de traslación en el que hemos trabajando no era una simple cantidad cualquiera, era también un operador, el operador K.
La aplicación del operador de traslación así definido arriba, actuando sobre una función de onda Ψ a su derecha, debe ser entonces:
Aún sin escribir a px en su forma explícita como un operador diferencial en esta expresión, lo que tenemos aquí se antoja formidable. ¿Cómo vamos a llevar a cabo la operación que está siendo especificada? La única forma de poder sacarle sentido a esto es desarrollando el operador exponencial como una serie de Taylor:
Desarrollando primero al operador de traslación sin expresar al operador diferencial del momentum en su forma explícita, haciendo A = -iapx/ħ se tiene:
Puesto que, operacionalmente:
metiendo entonces estas relaciones del operador del momentum en la expresión desarrollada para el operador de traslación, vemos que:
Simplificando:
Este es el operador que tenemos que aplicar sobre una función de onda Ψ(x) para desplazarla una distancia a con respecto a su posición original.
El siguiente paso consiste en someter a prueba el operador de traslación que hemos obtenido.
PROBLEMA: Aplíquese el operador de traslación a una función de onda representativa de una partícula libre manteniéndose la variable del tiempo constante.
La ecuación general de una onda plana móvil es:
Haciendo t.=.0 y manteniendo la variable del tiempo fija, la función de onda sobre la cual trabajaremos es la siguiente:
Podemos considerar esto último como la ecuación de onda de una partícula cuyo momentum px se conoce en forma precisa pero cuya posición exacta se desconoce (al extenderse la función de onda que representa a la partícula desde -∞ hasta +∞). Aplicando el operador de traslación a esta función de onda y desarrollando:
Esta es precisamente la función de onda original, pero desplazada a unidades hacia la derecha. Esto verifica que el operador de traslación que hemos obtenido es el operador correcto.
Para quienes no están muy familiarizados con las propiedades del número e pero que están familiarizados con la definición básica de la derivada infinitesimal, hay otra derivación alterna del operador de traslación en su forma exponencial que puede resultar más satisfactoria. Considérense los siguientes pasos, basados en las propiedades del operador de traslación que hemos visto arriba:
Despejando, esto último se puede escribir de la siguiente manera:
Podemos reconocer lo que aparece al lado izquierdo de la igualdad esencialmente como la derivada del operador de traslación con respecto al desplazamiento a, pudiendo por lo tanto representarlo en la forma convencional que se acostumbra en el cálculo infinitesimal, tras lo cual podemos efectuar un despeje para llegar a una ecuación diferencial que resultará familiar para muchos:
La ecuación diferencial que se tiene en la segunda línea está precisamente en la forma que nos conduce a una solución exponencial convencional, de acuerdo a la teoría de las ecuaciones diferenciales. Esta solución es el mismo resultado que se había obtenido arriba utilizando una composición de traslaciones:
Considerando un desplazamiento espacial llevado a cabo en tres dimensiones:
un operador de traslación más general, en el espacio tridimensional, será, efectuando traslaciones independientes en cada uno de los ejes coordenados Cartesianos:
Usando el operador de traslación tri-dimensional, supóngase que se lleva a cabo un desplazamiento espacial en una magnitud Δx sobre el eje-x Cartesiano:
Del mismo modo, supóngase que se lleva a cabo un desplazamiento espacial en una magnitud Δy sobre el eje-y Cartesiano:
Llevaremos a cabo ahora la evaluación del siguiente conmutador:
Efectuando el cálculo y despreciando términos de segundo orden en adelante:
Pero ya hemos visto arriba que las operaciones de traslación llevadas a cabo sobre ejes Cartesianos distintos (ortogonales) son conmutativas, lo cual implica que el conmutador con el cual hemos empezado debe ser igual a cero, lo cual a su vez implica que:
Este mismo resultado se puede obtener para cualquier otro par de ejes Cartesianos, lo cual podemos generalizar como:
De lo que no debe quedar duda alguna es que la razón principal por la cual obtuvimos esto es porque las operaciones de traslación para ejes distintos es conmutativa, o sea:
Este es otro resultado de importancia fundamental, ya que podemos ver que la razón por la cual los operadores diferenciales mecánico-cuánticos del momentum sobre ejes coordenados Cartesianos distintos conmutan es porque ello es una consecuencia directa del hecho de que los desplazamientos espaciales que se ven reflejados en los operadores de traslación también conmutan. Es por esto que es posible medir con precisión ilimitada las tres componentes px, py y pz del momentum de una partícula sin que entre en el panorama el principio de incertidumbre de Heisenberg. Es por esto que las tres componentes del momentum son observables compatibles. Sin embargo, cuando entremos a fondo en el estudio de las rotaciones, en virtud de que las rotaciones sucesivas llevadas a cabo sobre ejes coordenados Cartesianos distintos no conmutan, y esto traerá como consecuencia directa e inevitable la aparición de las relaciones de conmutación de Born para los operadores mecánico-cuánticos del momento angular, reduciendo a las tres componentes del momento angular a la calidad de observables incompatibles.
Un asunto que nos interesa explorar es el comportamiento de los valores esperados (esperanzas matemáticas) de las observables cuando se lleva a cabo una operación de traslación. Empezaremos con un operador de traslación actuando sobre un ket general de estado llevándose a cabo un desplazamiento espacial a:
La contraparte de esta operación, llevada a cabo en el espacio dual, usándose un bra en lugar de un ket, es la siguiente:
Tomando el producto interno de estas dos operaciones en la forma convencional, se tiene:
Como no se ha llevado a cabo desplazamiento alguno sobre observable alguna, esto simplemente nos confirma la conservación de la probabilidad. Ahora bien, la esperanza matemática de un operador mecánico-cuántico Q que representa a una observable física con respecto al ket general de estado que hemos usado arriba será, por definición:
Recurriendo a los ket y bra trasladados de arriba, la esperanza matemática de la observable trasladada será entonces:
La esperanza matemática de la observable Q trasladada, recurriendo a la base filosófica fundamental de la Mecánica Cuántica de reemplazar observables por operadores, lo cual nos permite considerar en este caso a Q como un operador de carácter general, nos va sugiriendo aquí otra posibilidad de enorme potencia teórica: la posibilidad de describir los cambios de un sistema físico mecánico-cuántico no mediante cambios llevados a cabo sobre una función de onda ψ sino sobre el operador que esté actúe sobre una función de onda. En otras palabras, en lugar de considerar al operador como inmutable y a la función de onda como algo variable, se consideraría al operador como algo variable, y a la función de onda como inmutable.
De acuerdo a lo que se acaba de obtener arriba, un operador de traslación puede ser utilizado no de una sola manera sino de dos maneras distintas:
(1) Actuando de la siguiente manera sobre una función de onda que está a su derecha para llevar a cabo el desplazamiento espacial de dicha función de onda:
(2) Actuando sobre un operador que está “aprisionado” a manera de “sanwich” de la siguiente manera entre el transconjugado del operador de traslación y el operador de traslación con la finalidad de obtener el operador trasladado:
Como lo iremos confirmando posteriormente, este uso dual es válido no sólo para el operador de traslación sino para una amplia gama de otros operadores distintos tales como el operador de evolución del tiempo y los operadores de rotaciones.
PROBLEMA: Suponiendo que el siguiente operador de traslación tridimensional en donde ρ es un vector de desplazamiento fijo:
produce el siguiente efecto sobre una función de onda Φ(r):
evalúese el efecto que la siguiente operación:
produce sobre un operador Q(r).
Sea una función de onda Ψ(r), y aplíquese sobre dicha función de onda el operador combinado:
Se ha hecho actuar arriba al operador de traslación sobre la función de onda Ψ(r) que está inmediatamente a su derecha, obteniéndose la función de onda trasladada espacialmente Ψ(r+ρ). En la última línea se ha hecho un reagrupamiento para resaltar el hecho de que el transconjugado del operador de traslación actuará tanto sobre el operador Q(r) como sobre la función de onda Ψ(r+ρ), lo cual producirá el siguiente efecto:
Se deduce entonces que:
Puesto que la función de onda puede ser una función de onda arbitraria cualquiera, lo anterior sólo podrá ser cierto si:
Este resultado nos confirma que se ha llevado a cabo una traslación espacial del operador Q(r), y nos dá también la prescripción general para llevar a cabo la traslación espacial de cualquier operador. El procedimiento para llevar a cabo la traslación espacial de un operador debe ser reminiscente del procedimiento T-1AT con el cual una matriz A es convertida en una matriz diagonal, excepto que aquí podemos estar hablando de operadores diferenciales en lugar de estar hablando de matrices.
PROBLEMA: Usando el operador de traslación en tres dimensiones, evalúese el siguiente conmutador:
Para la evaluación de este conmutador, recurriremos a la siguiente relación obtenida previamente en otras entradas (véase, por ejemplo, la entrada titulada “El espacio-posición y el espacio-momentum II”):
De este modo:
PROBLEMA: Usando el resultado del problema anterior, encuéntrese la manera en la cual cambiará el valor esperado de la posición bajo una operación de traslación.
La esperanza matemática de la posición sobre cualquiera de los tres ejes coordenados, usando un ket general de posición, se define como:
Considérese el resultado de la evaluación de la siguiente expresión:
La misma expresión puede ser evaluada de una manera distinta aplicando al pie de la letra la definición del conmutador:
Metiendo aquí el resultado obtenido previamente, se tiene:
Despejando, esto último se puede escribir como sigue:
Poniendo atención cuidadosa en lo que se tiene al lado izquierdo de la igualdad, puede apreciarse que se trata de la esperanza matemática del valor desplazado espacialmente sobre la coordenada en cuestión. O sea:
Puesto que este resultado es válido para las tres coordenadas Cartesianas, se pueden resumir las tres relaciones en una sola mediante el empleo de notación vectorial:
Un problema un poco menos trivial que el que se acaba de resolver consiste en determinar los cambios que pueden ocurrir o no ocurrir bajo una operación de traslación para otro tipo de operadores que no sea el operador de posición.
PROBLEMA: Detemínense los cambios que puedan ocurrir en el valor esperado del operador del momentum bajo una operación de traslación.
Usando el operador de traslación en tres dimensiones, evaluaremos primero el siguiente conmutador en donde pi es la componente del vector momentum p en cualquiera de los tres ejes coordenados rectangulares Cartesianos:
Para la evaluación de este conmutador, recurriremos a la siguiente relación obtenida previamente en otras entradas, siendo F(x) cualquier función del vector posición x:
Con esto se tiene:
para lo cual se han considerado a las tres componentes del vector de traslación l:
como cantidades constantes (representando un desplazamiento espacial fijo). Por lo tanto:
Aplicando la definición del conmutador en esto último:
lo cual nos dice que cada una de las tres componentes del momentum conmutan con el operador de traslación tridimensional. De este modo, aplicando este resultado podemos evaluar la esperanza matemática del operador del momentum trasladado bajo un desplazamiento espacial:
Esto nos confirma que las operaciones de traslación espacial no alteran el momentum de una partícula o de un sistema físico, un resultado que era de esperarse. Puesto que el resultado obtenido es válido para cada una de las tres componentes del momentum, podemos expresar el resultado general para todas las tres componentes Cartesianas del momentum la siguiente manera:
En la obtención del operador de traslación que se llevó a cabo más arriba, se supuso implícitamente como cierto algo que debe parecer obvio a primera vista: la homogeneidad del espacio. Suponemos que el espacio es homogéneo, lo cual significa que tiene la misma estructura en todos sus puntos. Esto es sinónimo con la suposición de que la solución a cierto problema físico es invariante bajo traslaciones espaciales. Un experimento Stern-Gerlach llevado a cabo en Nueva York debe dar los mismos resultados que el mismo experimento Stern-Gerlach llevado a cabo en Alemania o inclusive en la Luna. Formalmente, el principio de la homogeneidad del tiempo es expresado matemáticamente por el hecho de que la función clásica conocida como el Lagrangiano de un sistema de partículas permanece invariante cuando las coordenadas ri de las partículas son reemplazadas por ri+ai (en donde las ai son las componentes de un vector arbitrario constante no depende explícitamente del tiempo). Sin embargo, cualquiera que haya tomado conocimiento de los fundamentos de la Teoría Especial de la Relatividad ya sabe que el espacio no es una cosa absoluta, ya que depende de los marcos de referencia en los cuales se encuentren ubicados distintos observadores que se están moviendo el uno con respecto al otro. En cierta forma, esto es tomado en cuenta en el desarrollo de una forma más avanzada de Mecánica Cuántica conocida como la Teoría del Campo Cuántico en donde se incorporan los efectos de la Teoría Especial de la Relatividad dentro de las ecuaciones cuánticas. Pero hay otro problema más complejo tanto desde el punto de vista matemático como desde el punto de vista filosófico al tomar en cuenta a la Teoría General de la Relatividad y sus efectos en la curvatura del espacio-tiempo en la proximidad de campos gravitacionales de simetría esférica. Bajo esta perspectiva, dos observadores distintos, aún y cuando estén en estado de reposo absoluto el uno con respecto al otro, muestran alteraciones espaciales de longitud ante un tercer observador si ambos están situados a diferentes distancias del centro de gravedad. En principio, debe ser posible incorporar los efectos gravitacionales de la Teoría General de la Relatividad a la Mecánica Cuántica, y para campos gravitacionales débiles esperamos que las expresiones obtenidas concuerden con las expresiones mecánico-cuánticas que tanto éxito han tenido en sus poderes predictivos en innumerables experimentos. Pero el problema fundamental al principio del Tercer Milenio es que no ha sido posible llevar a cabo esta unión. Afortunadamente, los efectos gravitacionales en los fenómenos del mundo sub-microscópico solo adquieren relevancia bajo la acción de campos gravitacionales intensos como los que hay en la cercanía de los agujeros negros o los que hay en estrellas con una gran cantidad de masa, y se puede seguir trabajando en el planeta Tierra con lo que ya se tiene mientras se busca la manera de llevar a cabo la unión de la Teoría General de la Relatividad con la Mecánica Cuántica para crear una nueva Teoría del Campo Unificado que Albert Einstein no pudo lograr en vida.