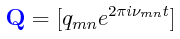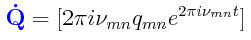Cuando Werner Heisenberg descubrió su “regla”, no se había dado cuenta de que la “regla de sumación” era de hecho la regla de multiplicación “renglón por columna” para dos matrices:
Más aún, su regla de sumación había sido desarrollada únicamente para la coordenada de la posición (la coordenada-x), sin extender el mismo procedimiento para el momentum. Fué Max Born el primero que reconoció a la regla de Heisenberg como la regla de multiplicación “renglón por columna” de dos matrices, y fué el primero que se dió cuenta de que lo que había descubierto Heisenberg era en realidad algo que tenía que ver con operaciones matriciales.
Heisenberg anunció al mundo su descubrimiento en julio de 1925. Pero ese descubrimiento estaba notoriamente incompleto. Heisenberg no se había dado cuenta de que sus arreglos cuadráticos en realidad eran matrices, y de que su regla era el resultado obtenido de una multiplicación de matrices. Más aún, la derivación de su regla provenía de la manipulación de la coordenada de la posición expresada en términos de una serie de Fourier, no se le había ocurrido hacer lo mismo en términos del momentum, como tampoco se le había ocurrido la posibilidad de que ambas cantidades pudieran estar inextricablemente ligadas.
En un resumen de memorias y recuerdos compartidos con su auditorio con motivo de su galardonamiento con el Premio Nóbel de Física el 11 de diciembre de 1954, Max Born mencionó lo siguiente en torno a su posterior intervención para tomar en sus manos lo que Heisenberg había dejado pendiente:
En Göttingen también tomamos parte en los intentos para destilar la mecánica desconocida del átomo extrayéndola de los resultados experimentales. La dificultad lógica se volvió cada vez más aguda... El arte de adivinar fórmulas correctas... fue llevado a una perfección considerable.
Este período fue llevado a una súbita conclusión por Heisenberg. Él... reemplazó el trabajo al tanteo por una regla matemática... Heisenberg proscribió la imagen de órbitas electrónicas de radios orbitales y períodos de rotación bien definidos, porque estas cantidades no son observables; él exigía que la teoría estuviese construída hacia arriba mediante arreglos cuadráticos... de transiciones de probabilidad... Para mí la parte decisiva de su trabajo es el requerimiento de que uno debe encontrar una regla mediante la cual a partir de un arreglo dado... el arreglo para el cuadrado (de la cantidad) pueda ser encontrado (o, en general, la multiplicación de tales arreglos).
Mediante la consideración de... ejemplos... él encontró esta regla... Esto fue en el verano de 1925. Heisenberg... tomó su descanso sabático... y me entregó su papel a mí para su publicación.
La regla de multiplicación de Heisenberg no me dejó en paz, y tras una semana de pensamientos y reflexiones intensas, de pronto recordé una teoría algebraica... Tales arreglos cuadráticos son bastante familiares para los matemáticos y se llaman matrices, en relación con una regla bien definida para la multiplicación. Apliqué esta regla a la condición cuántica de Heisenberg y encontré que estaba de acuerdo para los elementos diagonales. Era fácil adivinar cuáles deberían de ser los elementos que faltaban, a decir, nulos; e inmediatamente tuve ante mí la fórmula extraña:
Cuando al darse cuenta Max Born de que lo que Heisenberg había obtenido era en esencia algo que tenía que ver con operaciones matriciales, fué entonces cuando se le ocurrió también representar ambas coordenadas generalizadas de la mecánica clásica (q y p) como matrices Q y P, y para entonces ya estaba en su camino para establecer la relación de conmutación fundamental de la Mecánica Cuántica Matricial, su “extraña ecuación”.
Para llegar a su “extraña ecuación”, Born siguió los pasos tomados por Heisenberg, partiendo de la condición de cuantización Wilson-Sommerfeld de la teoría cuántica “vieja”, la cual ya se había anotado por sí sola unos triunfos preliminares además de tener la indudable ventaja de estar expresada en coordenadas generalizadas:
Usando la notación de punto puesto encima para denotar una derivación con respecto al tiempo, la condición de cuantización puede ser escrita de la siguiente manera (la notación del punto puesto encima denota diferenciación con respecto al tiempo):
en donde la integración se debe llevar a cabo sobre un período completo T del movimiento. Puesto que el período T de un movimiento, medido en segundos, es igual a la recíproca de la frecuencia ν, medida en unidades de seg-1, podemos escribir lo anterior de la siguiente manera:
Otra cosa que podemos hacer sobre esta expresión es llevar a cabo algo que seguramente provocará muchas dudas e inquietudes entre quienes ya se habían hecho a la idea del quantum en el cual al entero n sólo se le permite tomar valores enteros positivos. En ambos lados de dicha expresión, tomaremos la derivada con respecto a n:
Para cualquier estudiante del cálculo infinitesimal, la derivada de una función o expresión cualquiera está basada en el concepto del límite, bajo el cual la variable independiente con respecto a la cual se está derivando no sólo puede tomar cualquier valor posible, sino que se le hace tender hacia cero, o sea Δx→0. ¿Pero en el caso del número cuántico n que sólo puede tomar valores enteros positivos, cómo se puede justificar, el hacer Δn→0? En rigor de verdad, y hablando en términos estrictamente matemáticos, tal cosa no es posible. Y de hecho tampoco estamos haciendo tal cosa en la expresión anterior. Lo que estamos haciendo es darle validez a la expresión en el rango de los números cuánticos grandes, precisamente el lugar en donde adquiere plena validez el principio de correspondencia de Bohr, el mismo principio que fue utilizado por Heisenberg para obtener su “regla de multiplicación”. Más que hacer Δn→0, lo que estamos haciendo es Δn→1, pero siempre dentro del rango de los números cuánticos grandes. En comparación con un número cuántico de 50, darle a Δn un valor de 5 representaría la décima parte de dicho número cuántico. Pero en comparación con un número cuántico de 1,000,000, darle a Δn un valor de 2 representaría una fracción insignificante, representaría de hecho un infinitésimo (en comparación). Visto de otra manera, la diferencia entre los números cuánticos
250,000,000
y
250,000,003
es prácticamente insignificante, y en comparación el Δn de 3 se puede tomar como un infinitésimo. En el ámbito de los números cuánticos grandes, no es posible discernir ya una discretización de valores, y para fines prácticos podemos considerar esa región (en donde es aplicable el principio de correspondencia de Bohr) como un continuum en la cual se puede tomar la derivada con respecto a n.
Si tal y como lo hizo Heisenberg, representamos a la coordenada clásica de la posición q (medida a lo largo de un eje-x) mediante una matriz Q con cada uno de sus elementos definidos de la siguiente manera:
en donde los qmn son cada uno de los elementos de la matriz Q, entonces podemos suponer que al momentum clásico p también se le puede dar la siguiente representación matricial (en esencia, idéntica, excepto que las amplitudes pmn de cada elemento de la matriz son componentes de momentum en lugar de ser componentes de posición):
Tal y como lo hiciera Heisenberg trabajando únicamente sobre la coordenada posición, Born llevó a cabo la expansión de ambas coordenadas generalizadas expresándolas como series de Fourier infinitas:
Habiendo definido esto, el siguiente paso consiste en tomar la derivada con respecto al tiempo de la coordenada de la posición generalizada q, y llevar a cabo la integración de conformidad con la condición de cuantización Wilson-Sommerfeld.
Para poder continuar adelante, Born al igual que Heisenberg tuvo que apelar al requerimiento de realidad habido el hecho de que las cantidades imaginarias (i = √-1) no pueden ser medidas en el laboratorio, ni se les puede dar interpretación física alguna, sólo a las cantidades reales se les puede dar un significado en el mundo real. Born escogió tomar el conjugado complejo de la serie Fourier para la posición, con lo cual su “requerimiento de realidad” para una posición medida a lo largo de una coordenada-x vendría siendo:
x(n, -τ) = x*(n, τ)
o bien, en coordenadas generalizadas:
q(n, -τ) = q*(n, τ)
De este modo, llevando a cabo la integración como lo pide la condición de cuantización Wilson-Sommerfeld, y utilizando el “requerimiento de realidad”, Born obtuvo lo siguiente:
Ahora tomaremos en ambos lados de esta expresión la “extraña derivada” mencionada arriba, en el sobreentendido de que el proceso de derivación será válido únicamente en la región en donde el principio de correspondencia de Bohr es válido, la región de los números cuánticos grandes:
o bien:
Es aquí en donde recurrimos al principio de correspondencia, que en una de las formas en las cuales puede ser escrito nos permite aseverar lo siguiente válido:
De este modo, podemos continuar con nuestro desarrollo:
“Limpiando” el lado izquierdo de los conjugados complejos, haciendo de paso a la sumatoria válida de τ=0 a τ=+∞, es así como obtenemos lo siguiente:
Obsérvese que en el segundo término en el lado izquierdo de la igualdad se ha intercambiando el orden en el que están escritos p y q, esto con la finalidad de destacar algo que si no es obvio en este momento seguramente será obvio en los siguientes pasos.
En el lado izquierdo, la sumatoria de los dos productos se puede subdividir en dos sumatorias, conduciéndonos a:
A estas alturas, para quienes conocen y han manejado la definición esencial del producto de dos matrices, debe resultar evidente que lo que tenemos en el lado izquierdo son dos productos matriciales, a saber:
Esto nos conduce directamente a nuestra conclusión final:
Esta es la “extraña ecuación” que Born tenía ante sí después de haber llevado a cabo los pasos que se han reproducido aquí. Es la ecuación cuyo descubrimiento le mereció el haber sido galardonado con el Premio Nóbel. Es la misma ecuación puesta como justo homenaje en el epitafio de su tumba. Max Born anunció al mundo su descubrimiento compartiéndolo en un trabajo conjunto con Pascual Jordan publicado en septiembre de 1925, a escasos dos meses después de que apareciera publicado el papel en el que Heisenberg anunció su famosa “regla de multiplicación”.
El lector alerta podrá objetar aquí una cosa: en todo lo que hemos llevado a cabo, el resultado final que hemos obtenido en realidad es válido únicamente para los elementos diagonales de los productos matriciales resultantes, los que van puestos en el renglón n y en la columna n de la diagonal principal de las matrices resultantes. ¿Y los demás elementos, los elementos no diagonales?
Tras haber obtenido su “extraña ecuación”, Born conjeturó que ésta debería ser válida también para los elementos no diagonales, como nos lo menciona él mismo en las palabras suyas que han sido citadas arriba. Y no llevó mucho tiempo el comprobar que así era, en efecto.
En la obtención de la “extraña ecuación” de Max Born, se han utilizado las coordenadas generalizadas propias de la mecánica clásica. El haber obtenido un resultado que ha sido confirmado cientos de miles de veces en los más extenuantes y sofisticados experimentos de laboratorio a partir de definiciones clásicas nos puede llevar a sospechar que mucho de lo que se ha desarrollado dentro de la mecánica clásica (específicamente, la mecánica Lagrangiana y la mecánica Hamiltoniana) tendrá muchas contrapartes en la Mecánica Matricial. Y Max Born fue uno de los primeros que descubrió que así era, en efecto. Sin embargo, hay una diferencia fundamental entre la mecánica matricial cuántica y la mecánica clásica. Mientras que en la segunda manejamos exclusivamente funciones continuas suaves, en la mecánica matricial cuántica la contraparte está en las matrices que vienen siendo en realidad operadores.
En la mecánica clásica, el Hamiltoniano H de un sistema (de la cual deriva su nombre el operador matricial que representa los niveles de energía permisibles en el caso de una partícula atómica o subatómica confinada a una región cerrada) es una función que depende tanto de la coordenada generalizada posición q como de la coordenada generalizada momentum p así como del tiempo. Para un sistema conservativo (en el cual no hay disipación de energía), el Hamiltoniano clásico es función única y exclusivamente de la coordenada generalizada posición q como de la coordenada generalizada momentum p, o sea:
H = H(q, p)
Si podemos definir dos matrices Q y P las cuales son respectivamente la matriz posición y la matriz momentum en nuestra nueva Mecánica Matricial, y si el Hamiltoniano clásico está definido en función de la coordenada generalizada posición q y la coordenada generalizada momentum p, ¿qué nos detiene de definir un Hamiltoniano matricial? Nada. Es así como podemos postular como una realidad lo siguiente:
H = H(Q, P)
Y los valores característicos eigen del operador Hamiltoniano matricial para algún sistema físico en particular como el oscilador armónico simple deberán ser a su vez los valores permisibles de la energía (las observables medibles en el laboratorio) que puede tomar un oscilador armónico simple construído con partículas sub-atómicas.
Por otro lado, el Hamiltoniano clásico está relacionado con el Lagrangiano clásico de un sistema mediante la definición:
en donde cada pi está dado por:
Si de la definición del Hamiltoniano resolvemos para el Lagrangiano L, entonces del principio de Hamilton que nos asevera que el desarrollo de un sistema físico será tal que la integral del Lagrangiano con respecto al tiempo tomará el camino que produzca el valor mínimo para todas las integrales posibles:
tenemos entonces la siguiente condición de extremalización:
No se requiere de mucho esfuerzo para conjeturar que, en la Mecánica Matricial, el Lagrangiano matricial L a ser extremizado será:
en donde:
Born comprobó, mediante la extremalización de la traza del Lagrangiano matricial (los elementos diagonales) que utilizando la definición aceptada -para funciones matriciales- de la “derivada de una matriz con respecto a otra matriz” se obtenían las siguientes dos ecuaciones matriciales del movimiento:
Compárense estas dos ecuaciones matriciales con las ecuaciones de Hamilton (clásicas, no-matriciales):
Este tipo de analogías nos permiten suponer que si partimos de los resultados de la mecánica clásica convencional, podemos obtener muchos resultados útiles y válidos dentro de la Mecánica Matricial. Sin embargo, es prudente tener cuidado en los cambios que se pueden suscitar, porque aunque las ecuaciones de Hamilton trabajan bien para la mecánica clásica no se les puede traducir ciegamente hacia la Mecánica Cuántica por el simple hecho de que mientras que en la mecánica clásica se pueden conocer simultáneamente la posición exacta y el momentum exacto de cualquier objeto, en la Mecánica Clásica no es posible lograr tal cosa cuando se trata de partículas atómicas y sub-atómicas, lo cual implica que no es posible el poder especificar el momentum de una partícula en función de su momentum, o sea no es posible escribir algo que se pueda leer como p(q).
Después de leer el papel original de Heisenberg publicado en julio de 1925, en el otoño del mismo año el físico-matemático Paul Adrien Maurice Dirac trabajando desde Cambridge recordó que ya había visto dentro de la mecánica clásica algo parecido a la no-conmutatividad que aparecía en la “nueva” Mecánica Cuántica. Este “algo” eran los corchetes de Poisson (Poisson brackets). Dadas dos funciones F y G que dependen de las coordenadas generalizadas de la posición qα y de los momentums pα así como del tiempo:
F = F(qα, pα, t)
G = G(qα, pα, t)
G = G(qα, pα, t)
se define un corchete de Poisson de la siguiente manera:
PROBLEMA: Demostrar que para un corchete de Poisson se cumple la propiedad de anticonmutatividad:
[F, G] = - [G, F]
Recurriendo directamente a la definición del corchete de Poisson, tenemos lo siguiente llevando a cabo un simple intercambio:
Esto demuestra que el corchete de Poisson no obedece la regla de conmutatividad del álgebra ordinaria.
PROBLEMA: Demostrar la propiedad distributiva para los corchetes de Poisson:
[F1 + F2, G] = [F1, G] + [F2, G]
Nuevamente, recurrimos a la definición del corchete de Poisson:
Simplificando:
Finalmente:
[F1 + F2, G] = [F1, G] + [F2, G]
PROBLEMA: Recurriendo a las ecuaciones clásicas de Hamilton definidas arriba, demuéstrese que:
De la definición matemática para una derivada total, podemos escribir lo siguiente:
Usando las ecuaciones canónicas de Hamilton:
podemos reescribir a dg/dt de la manera siguiente:
Esto último lo podemos compactar recurriendo a los corchetes de Poisson:
PROBLEMA: Mediante los corchetes de Poisson, demuéstrese que:
[pk, pj] = 0
De acuerdo a la definición de los corchetes de Poisson, tenemos lo siguiente:
Puesto que los momentums generalizados son una cosa distinta a las coordenadas generalizadas, se tiene entonces:
∂pk/∂qα = 0__para todo k y α
con lo cual lo escrito en rojo arriba es igual a cero, resultándonos en:
[pk, pj] = 0
PROBLEMA: Mediante los corchetes de Poisson, demuéstrese que:
[qk, qj] = 0
De acuerdo a la definición de los corchetes de Poisson, tenemos lo siguiente:
Puesto que las coordenadas generalizadas son una cosa distinta a los momentums, se tiene entonces:
∂qk/∂pα = 0__para todo k y α
con lo cual lo escrito en rojo arriba es igual a cero, resultándonos en:
[qk, qj] = 0
PROBLEMA: Mediante los corchetes de Poisson, demuéstrese que:
[qk, pj] = δkj
De acuerdo a la definición de los corchetes de Poisson, tenemos lo siguiente:
De nueva cuenta, puesto que los momentums generalizados son una cosa distinta a las coordenadas generalizadas, se tiene entonces:
∂qk/∂pα = 0__y__∂pj/∂qα___para todo k, j y α
con lo cual lo que se ha destacado arriba en rojo se cancela, más no así el primer término, en donde usando el delta de Kronecker se ha resumido el hecho de que las componentes de las coordenadas generalizadas y los momentums generalizados son medidos a lo largo de coordenadas ortogonales independientes (en coordenadas rectangulares Cartesianas, esto significa que ∂x/∂y y ∂z/∂x, por ejemplo, son iguales a cero):
∂qm/∂qn = 1__ para m = n
∂qm/∂qn = 0__ para m ≠ n
∂qm/∂qn = δmn
∂qm/∂qn = 0__ para m ≠ n
∂qm/∂qn = δmn
y:
∂pm/∂pn = 1__ para m = n
∂pm/∂pn = 0__ para m ≠ n
∂pm/∂pn = δmn
∂pm/∂pn = 0__ para m ≠ n
∂pm/∂pn = δmn
Juntando ambos deltas de Kronecer en uno solo, se concluye que:
[qk, pj] = δkj
La analogía de la no-comutatividad entre la “extraña ecuación” obtenida por Max Born y la no-conmutatividad de los corchetes de Poisson fue lo que llevó a Dirac a tomar la relación de Born:
y tras simplificar la constante multiplicativa en el lado derecho de la igualdad introduciendo la “h barrada” ħ = h/2π (conocida también como la h de Dirac) escribiendo:
QP - PQ = iħI
Dirac introdujo su conmutador dentro de la Mecánica Cuántica utilizando deliberadamente los mismos paréntesis rectangulares que los utilizados en los corchetes de Poisson:
[Q, P] = iħI
No le costó mucho trabajo a Dirac darse cuenta de que varios de los resultados obtenidos en la Mecánica Matricial a partir de la relación de Born se pueden obtener de la contraparte clásica mediante la simple introducción del factor iħ, asentando la siguiente equivalencia para convertir un resultado clásico a un resultado cuántico:
PROBLEMA: Obtener la relación fundamental de Born a partir del resultado clásico.
Como vimos en el último de los problemas resueltos arriba, tenemos que clásicamente:
[qk, pj] = δkj
Para convertir esta ecuación clásica a la ecuación matricial cuántica correspondiente, establecemos las siguientes correspondencias de cantidades clásicas a cantidades matriciales:
qk → Q
pj → P
δkj → I
pj → P
δkj → I
Con esto:
[qk, pj]clásico = δkj
([Q, P]cuántico)/iħ = I
[Q, P]cuántico = iħI
([Q, P]cuántico)/iħ = I
[Q, P]cuántico = iħI
De este modo, y procediendo en orden inverso a como se ha mostrado arriba, es posible derivar la mecánica clásica a partir de la Mecánica Cuántica. Sin embargo, no es posible hacer lo inverso, esto es, derivar la Mecánica Cuántica de la mecánica clásica, en virtud de que hay parámetros físicos que no tienen contraparte alguna en la mecánica clásica, y al decir esto lo hacemos teniendo en mente el spin del electrón y de todas las demás partículas atómicas que poseen esta propiedad.
A continuación tenemos algunas de las memorias de Dirac en donde nos comparte varias de sus impresiones y reflexiones sobre aquella época:
Había muchas reuniones entre los estudiantes de Cambridge para discutir problemas científicos, y entre ellas estaba el Club Kapitza.
Kapitza... estableció un club de físicos... Nos reuníamos los martes por las tardes después de la cena... Ese no era un tiempo muy conveniente para mí porque usualmente yo estaba algo soñoliento después de la cena. Yo hacía mi trabajo durante las mañanas... y al acercarse la conclusión del día yo estaba más o menos opaco, especialmente después de la cena...
En el verano de 1925, Heisenberg vino a Cambridge, y dió una plática al Club Kapitza. Hacia el final... habló acerca de unas ideas nuevas suyas. Para este tiempo yo ya estaba simplemente demasiado exhausto para poder seguir lo que decía, y no lo pude tomar dentro de mí. Estaba hablando acerca de los orígenes de sus ideas de la nueva mecánica. Pero yo fallé completamente en darme cuenta de que en realidad estaba introduciendo algo muy revolucionario. Después olvidé totalmente lo que dijo en relación a su nueva teoría. Inclusive llegué a convencerme de que no había dicho nada acerca de ello, pero otras personas que estuvieron presentes en esta reunión del Club Kapitza me aseguraron que sí había hablado de ello... y yo simplemente tengo que aceptar que él realmente habló acerca de ello y que yo fallé totalmente en responder a esto, y así me perdí una gran oportunidad de empezar en ello de inmediato.
Fue un poco después cuando yo realmente empecé en la nueva teoría de Heisenberg. Heisenberg le envió [su papel] a Fowler... Fowler me lo remitió con una pregunta, ‘¿Qué opinas acerca de esto?’ Al principio yo no estaba muy impresionado con su trabajo. Me parecía ser demasiado complicado. Simplemente no ví el punto principal, y en lo particular su derivación de condiciones cuánticas parecía demasiado estirada, así que lo hice a un lado considerándolo sin interés alguno. Sin embargo, una semana o diez días después regresé a este papel de Heisenberg y lo estudié con mayor detalle. Y de pronto me dí cuenta de que contenía la llave de la solución completa...
Yo estaba trabajando con estas nuevas variables, las variables cuánticas, y a mí me parecían ser unas cantidades físicas muy misteriosas, e inventé una palabra nueva para describirlas. Las llamé números-q, y llamé a las variables ordinarias de las matemáticas números-c, para distinguirlas. La letra q significa quantum... y la letra c significa clásico o tal vez conmutantes. Entonces procedí a construír una teoría de estos números-q...
Ahora bien, yo no sabía nada acerca de la verdadera naturaleza de estos números-q. Yo pensaba que las matrices de Heisenberg eran simplemente un ejemplo de números-q; tal vez los números-q eran algo más general. Todo lo que uno sabía acerca de los números-q es que obedecían una álgebra que satisfacía los axiomas ordinarios, excepto el axioma conmutativo de la multiplicación... No me preocupé en lo absoluto por encontrar una naturaleza matemática precisa para los números-q.
Ví que la no-conmutación era la característica dominante de la nueva teoría de Heisenberg. Era más importante que la idea de Heisenberg de construír una teoría en términos de cantidades estrechamente conectadas con resultados experimentales. Así fuí conducido a concentrarme en la idea de la no-conmutación y ver cómo la dinámica ordinaria que la gente había estado usando hasta entonces debía ser modificada para incluírla.
De los corchetes de Poisson es posible obtener otras relaciones que pueden ser “traducidas” ventajosamente de inmediato a la Mecánica Cuántica, entre ellas:
[A,A] = 0
[A,[B,C]] + [B,[C,A]] + [C,[A,B]] = 0 (Identidad de Jacobi)
[A,BC] = [A,B]C + B[A,C]
[AB,C] = A[B,C] + [A,C]B
[ABC,D] = AB[C,D] + A[B,D]C + [A,D]BC
[AB,CD] = A[B,CD] + [A,CD]B = A[B,C]D + AC[B,D] + [A,C]DB + C[A,D]B
[[A,C],[B,D]] = [[[A,B],C],D] + [[[B,C],D],A] + [[[C,D],A],B] + [[[D,A],B],C]
PROBLEMA: Evalúese:
[Q², P²]
de dos maneras distintas: (1) recurriendo directamente a la ecuación fundamental de Born, y (2) partiendo de los corchetes de Poisson haciendo la conversión de la forma clásica a la forma cuántica utilizando la regla de Dirac.
(1) Trabajando sobre la relación dada:
[Q², P²] = [Q², PP] = [Q², P]P + P[Q², P]
Pero ya habíamos obtenido previamente el resultado:
[Q², P] = 2iħQ
Entonces:
[Q², P²] = (2iħQ)P + P(2iħQ)
[Q², P²] = 2iħ(QP + PQ) = 2iħ{Q, P}
en donde hemos utilizado en el último paso los corchetes del anticonmutador.
(2) En base a los corchetes de Poisson, tenemos lo siguiente:
En base a la regla de Dirac, tenemos:
en donde nuevamente hemos utilizado en la última expresión los corchetes propios del anticonmutador (los cuales no deben ser confundidos en ningún momento con los corchetes de Poisson).
PROBLEMA: Sabiendo que en la mecánica clásica, para una función F(p,q) que no depende explícitamente del tiempo, la siguiente relación es válida:
obténgase la contraparte cuántica usando la regla de Dirac.
De acuerdo con la regla de Dirac, la relación cuántica será la siguiente:
Esta resulta ser una relación muy importante que amerita el ser estudiada por separado, mejor conocida como la ecuación del movimiento de Heisenberg.